In Time Reborn: From the Crisis in Physics to the Future of the Universe (2013) (by the theoretical physicist Lee Smolin) there’s a chapter called ‘Doing Physics in a Box’. That chapter is the basis of this piece.

Doing physics in a box has a long history.
According to Lee Smolin himself, it goes back to Kepler, Galileo, Descartes and Newton in the 16th and 17th centuries.
But what do the words ‘doing physics in a box’ mean?
To Smolin, they mean that these scientists “learned to [] isolate little pieces of the world, examine them, and record the changes to them”.
So how did they do this? Smolin writes:
“They showed us how to display the records of these motions in simple diagrams whose axes represent the position and times in a way that is frozen and hence amenable to being studied at our leisure.”
[Smolin’s reference to frozen time hints at another major concern of his — the reality of time.]
Ironically, some of the thought-experimental “boxes” of physics are literal boxes.
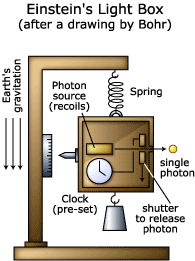
For example, we have Erwin Schrödinger famous cat-in-a-box thought experiment and Albert Einstein’s “light box” physical experiment. Interestingly enough, both experiments show the impact of outside forces on the boxes. (This is something which Smolin will stress later.) In the cat-in-the-box case, outside disturbances can or do “collapse the wave function”. Or as the chemist and science writer Philip Ball puts it:
“Schrödinger’s cat might be placed inside a sealed box, but there must be air in there for the cat to have any chance of staying alive. And the cat is resting on a surface of some kind, exchanging heat with it.”
Ball then admits that
“[i]f the environment is included at all in most scientific theories or analyses of experiments, it’s often simply considered to be the source of a little random disturbance, which can, with sufficient care, be kept to a minimum”.
Then comes this warning:
“But in quantum mechanics [] the environment has a central role in how things happen.”
As for Einstein’s light-box experiment, let science writer Manjit Kumar explain the problem:
“[] Bohr held that any measurement of the position of the light box would lead to an inherent uncertainty in its momentum, because to read the scale would require it to be illuminated. The very act of measuring its weight would cause an uncontrollable transfer of momentum to the light box because of the exchange of photons between the pointer and the observer causing it to move.”
“In his desperation to destroy the Copenhagen view of quantum reality, Einstein had forgotten to take into account his own theory of general relativity. He had ignored the effects of gravity on the measurement of time by the clock inside the light box.”
Later in this piece, the philosopher Nancy Cartwright specifically confronts Galileo’s “little piece[] of the world” — a ball on an inclined plain (i.e., a ramp). However, Smolin himself concentrates on quantum pieces of the world.
Lee Smolin: Doing Physics in a Quantum Box

The words “quantum box” are used because Smolin focuses on such a thing. He says that the “application of quantum mechanics appears to be limited to isolated systems”. Yet “[i]t’s [still] an extension of the Newtonian paradigm — of doing physics in a box”. Nonetheless, he mentions “classical” (or macro) boxes too.
Smolin has two important things to say about the experiments of physics:
1) That what he calls “subsystems” (or “isolated systems”) are inevitably part of the entire universe — therefore they’re also affected by the whole universe.
2) That experiments are extremely artificial constructs. (The most artificial aspects are the selected “initial conditions” of the experiment.)
Initial Conditions
As for initial conditions, Smolin writes:
“When we do an experiment in a laboratory, we control the initial conditions. We vary them to test hypotheses about laws.”
Then comes Smolin’s very particular addition:
“But when it comes to cosmological observations, the initial conditions were set in the early universe, so we must make hypotheses as to what those were.”
The words above highlight Smolin’s larger cosmological concerns.
Not only does Smolin emphasise the fact that “closed systems” are actually “open systems” delimited for the purpose of experiment (i.e., open to the entire universe!), he also notes that the present universe’s own initial conditions “were set in the early universe”.
Smolin supplies us with more details on initial conditions. Firstly, they determine the beginning of any experiment. Smolin writes:
“You specify which history describes a particular experiment when you give the initial conditions. Thus, to predict the future or explain something, it’s not enough to know the laws; you must also know the initial conditions. In laboratory experiments this is easy, because the experimenter prepares the system to start in some particular initial condition.”
Smolin (in the above) writes that “it’s not enough to know the laws”. He then cites “Galileo’s law of falling bodies”. This states that thrown balls (in this case) will “trace a parabola”.
So what were the initial conditions of this act of ball-throwing? And “which parabola” will be exemplified? Smolin says that the
“answer is determined by how fast and at what angle and from which location he threw the ball — that is, by the initial conditions”.
Earlier on Smolin had said that
“one law has an infinite number of solutions, each of which describes a possible history of the system in which the laws are satisfied”.
Thus, in the ball-throwing example, we have the “one law” which is Galileo’s law of falling bodies. In the case of Danny throwing the ball, its “history” is “determined by how fast, at what angle and from which location he threw the ball”. This is a single “solution” to Galileo’s law of falling bodies.
Isolated and Open Boxes
Let Smolin define an “isolated system”. He writes:
“A subsystem of the universe modeled as if it were the only thing in the universe, neglecting everything outside it, is called an isolated system.”
In a certain sense, it seems incredible that physicists would treat a subsystem “as if it were the only thing in the universe”. Of course physicists obviously know that their subsystem isn’t the only thing in the universe. However, for the purpose of the experiment, that is indeed how it is seen. That raises the question as to why it’s seen that way.
Now if we have isolated systems, we must also have systems which aren’t isolated. These are called “open systems”. Smolin writes:
“To one extent or another, subsystems of the universe are always what physicists call open systems. These are bounded systems that interact with things beyond those boundaries.”
Again, it seems obvious that no subsystem (or “isolated system”) can really be bounded. It can be treated as if it were bounded; though clearly it isn’t “in reality”. Yet, in many respects, treating the entire universe as part of an experiment or subsystem (which is Smolin’s concern) doesn’t make much sense. Or at least in doesn’t make much sense for practical (or everyday) scientific purposes.
Interestingly, in the context of experiments, open systems become isolated systems. That is, in order to do an experiment, the open system must be made into a isolated system. In Smolin’s words:
“A great deal of the craft of experimental physics consists in turning open systems into (approximately) isolated systems. We can never do this perfectly.”
The problem here is that physicists need to (as Smolin puts it) “shield [their] experiments from contamination from outside vibrations, fields, and radiation”. In addition, what is important to decipher is “[w]hat are the forces that the system is subject to in each configuration”. What’s more,
“[f]or many experiments, this suffices, but some experiments are so delicate that they are affected by noise from cosmic rays hitting the detectors”.
This particular problem can be solved by putting the laboratory “in a mine several miles underground” in order to “detect neutrinos from the sun”. Smolin continues:
“Neutrino detectors buried deep in the ice of the South Pole record neutrinos that have entered at the North Pole and travelled all the way through the Earth.”
And then there’s gravity and gravitational waves. Smolin ends:
“In principle, nothing can screen out the force of gravity or stop the propagation of gravitational waves, so nothing can be perfectly isolated. I discovered this important point during my PhD studies. I wanted to model a box that contained gravitational waves bouncing back and forth inside, but my models kept failing, because the gravitational waves passed right through the walls.”
The final upshot of all this is to realise that
“[t]o incorporate everything that might impinge on our laboratory from the outside would require a model of the whole universe”.
And, because of that, we must “base our physics on approximations”.
Truncations of Nature
Smolin often uses the words “truncations of nature”.
This idea closely parallels his notion of isolated systems in that nature is truncated (or simplified) in the experiments of physicists. In addition, the theories of physics are also truncated (such as, according to Smolin, the Standard Model of Particle Physics and General Relativity).
These truncations aren’t all about factoring out irrelevant details — which could be huge in extent. No; truncations factor out (or so Smolin argues) factors that may well be hugely important. Still, Smolin accepts that truncations are necessary when it comes to both the experiments and the theories of physics. Nonetheless, both cosmologically and philosophically, there’s a larger picture which needs to be considered. It needs to be considered not only for philosophical or cosmological reasons: it also needs to be considered because the boxes of physics may well be sending us in the wrong direction.
One truncation offered by Smolin
“is all about designing experiments to isolate and study a few degrees of freedom, ignoring the rest of the universe”.
That’s a truncation at the level of experiment. We also have truncations at the level of theories. Thus:
“All the theories we work with, including the Standard Model of Particles Physics and general relativity, are approximate theories, applying to truncations of nature that include only a subset of the degrees of freedom in the universe. We call such an approximate theory an effective theory.”
One way we can look at this is to say that we never have absolute (or total) truth in physics. Indeed, as many physicists and philosophers have argued over the years, that’s a good thing too. Thus if these theories weren’t “approximate”, then they’d be final and complete. And if they were final and complete, then physics would come to an end (at least in the domains in which all this is applied). Thus we have the pragmatic (or instrumentalist) term “effective theory” instead.
************************************
Nancy Cartwright: Doing Physics in a Classical Box

In order to draw out regularity and systematicity from experiments, the American philosopher Nancy Cartwright says that
“it takes an enormous amount of effort in special background conditions in special circumstances before you get regular repeatable behaviour”.
This highlights the stress which Smolin too puts on initial conditions.
To put the point crudely: if you change the initial (or background) conditions (which aren’t the same thing), you change everything. This also highlights the selection process which experimenters need to indulge in — which seems somewhat obvious really.

And then Smolin himself makes similar points in his book The Trouble With Physics: the Rise of String Theory. In that book he writes:
“It is often the case that surprising experimental results are not confirmed when other experimentalists repeat the experiment. This does not mean someone is being dishonest. Experiments on the edge of what is possible are always hard to replicate, and it is typically difficult to separate noise from a meaningful signal.”
All this clearly goes against the rather naive idea that physics is all about observation and the consequential making sense of what is observed. In other words, physics is also about “asking nature questions” and “manipulating nature”.
A Ball on an Inclined Plane
Nancy Cartwright gives her own example of the artificiality and specificity of experiments in the following:
“[] I think that you learn about certain situations or certain properties, what capacities they have, and you can also learn about the capacities they have by putting them in very specific circumstances — like, if you put a ball on an inclined plane, and make it as frictionless as possible, and you try to learn from that about the capacity of something with an inertial mass, say, to keep moving unless acted upon by a force to make it stop.”
Clearly, this particular experiment is a long way from Smolin’s isolated systems in that it’s dealing with (as J.L. Austin put it) “medium-sized dry goods”, not subatomic particles, forces, fields, radiation, etc. In any case, there are two things one can learn about the capacities of “certain situations or certain properties”. Namely:
1) We can discover what capacities are prevalent only in certain situations. And,
2) The capacities are displayed “by putting them in very specific circumstances”.
One can argue that situations or properties never have certain capacities “in themselves” because neither situations nor properties are ever entirely taken as they are in themselves. That is, both situations and properties are always embedded in particular contexts (or sets of conditions) and can never be found outside of them. Thus properties and situations act the way they act precisely because they’re in specific contexts (or conditions). It follows that they never act the same in all contexts and in all sets of conditions.
In physics, these conclusions will work against our modalising (i.e., thinking in terms of necessities, etc.) tendencies and the penchant to think in terms of universal generalisations. Thus, in the case of Cartwright’s own example of a ball on an inclined plane (which is as frictionless as possible), we’ll not always be able to come across frictionless planes (or even frictionless balls for that matter). Basically, this is a scientific set-up. It’s an experiment. However, if we don’t construct these initial conditions, then we’ll never learn about the capacity of some given x. (Say, how an inertial mass will “keep moving unless acted upon by a force to stop it”.) Perhaps frictionless planes don’t ever occur naturally — or at least not often. So this experiment (or artificial set-up) may never actually be replicated in nature — at least not to the full extent required to see what happens to balls when placed upon an inclined plane. This doesn’t mean that we don’t learn something about nature — even if nature never includes any planes which are frictionless. (Do we find balls in nature? Are they “natural kinds”?)
One of the problems with these experiments (or set-ups) is that one mustn’t only select what it is one wants to find out: one must also select the circumstances and conditions which will tell you what it is you want to find out. Different initial conditions will tell you different things. And even the same initial conditions can tell you different things depending on what it is one is looking for. As Cartwright puts it:
“Now, that characterising behaviour is often associated with constructing some special circumstances in which that characterising behaviour is exhibited, or almost or approximately exhibited, like the frictionless plane. But the question is, why are those circumstances particularly interesting circumstances? What’s so special about them — they’re after all just some circumstances: you could have this degree of friction, that degree of friction, you might not think about friction at all but something else, you might paint the inclined plane red [].”
This simply means that the initial conditions must be selected in the first place. Not only that: evidently different initial conditions will produce different effects (or further conditions). In addition, the very same initial conditions may result in different conclusions for the experimenter depending on the questions he wants answering or the things he wants to test. Thus there’s a selection process involved all the way down the line: from the selection of initial conditions to how the same (or different) initial conditions (or their consequences) are interpreted by the scientific experimenter.
Pure Observations?
All this shows us that there are no such things as pure observations (or pure “observations sentences” — as the logical positivists, such as Rudolf Carnap, believed). The same set of conditions — and even the same set of observations — will be interpreted in different ways by different observers (or experimenters). That’s because they bring along with them different theories (or different sets of assumptions) through which they interpret the same observations (or the same scientific data). Not only do experimenters bring along with them different theories (or a different set of assumptions): the theory they arrive at (or the confirmations they acquire) will result in different theoretical interpretations of what it is they’ve observed, experimented upon or tested.
In addition, “theory is always underdetermined by all the data”. That is, the very same data (observational or otherwise) may — or will — result in different theoretical interpretations depending on what the observer wants to know, etc. Even if different observers both want to bring about a frictionless plane (as in Cartwright’s example), the existence of a frictionless plane alone won’t guarantee that different observers (or experimenters) will make the same theoretical interpretations of the same data they have in front of them.
In Cartwright’s words, “why are those circumstances particularly interesting circumstances?” Of course what’s interesting to one scientific observer (or experimenter) won’t necessarily be interesting to another. Again, it depends on their prior interests and what it is they want from the experiment.
For instance, both observers may have some kind of frictionless plane. However, what if one observer wants to (as Cartwright puts it) “paint the inclined plain red?”. This may seem like a silly example. However, there may be some obscure reason for wanting to paint the inclined plain red. Perhaps the wavelengths of the colour red have some very slight affect on the frictionless plane. Alternatively, perhaps the experimenter is more interested in the physical nature of the colour red when it’s in conjunction with different materials. The point is that we can’t rule out this outré example.
Manipulating Nature: Distortions and Interferences
Cartwright’s main point about these variable issues is that they can be divided into two components. As she puts it:
“[W]e have these two concepts working at once — we have the concept of a capacity and its characterising behaviour, and then we have the concept of interference and distortion and the idea here is that you deploy your concepts of interference and distortion to come up with instances of the characterising behaviour, and the whole point about the characterising behaviour is that it’s behaviour that you learn how to change systematically in order to account for what happens in more complicated circumstances.”
The point is that these distortions and inferences of “characterising behaviour” will tell us something about such characterising behaviour and the dispositional capacities which underlie them. That if, if such-and-such a thing distorts the initial conditions under scrutiny, then we’ll learn something about these initial conditions and the properties involved in them. Similarly, if we can interfere with these initial conditions, and the capacity-laden properties involved in them, then that interference will tell us something about such properties and the initial conditions.
So what things interfere and distort the properties and initial conditions? Why do they do so? Why are certain aspects of the initial conditions or properties unchanged by such distortions or acts of interference? What can we learn about the capacities of the properties through such distortions and acts of interference? And so on.
Conclusion
Finally, not only can we introduce distortions and interferences to affect the properties (or the initial conditions) in order to acquire new information about them: we’ll also “learn how to change [them] systematically in order to account for what happens in more complicated circumstances”.
All this shows us that science isn’t only about observation, testing, confirmation and the creation of theories: it’s also about the manipulation of nature. By such manipulations (such as distortions and acts of interference) we learn much more about nature than we would do simply by observing natural phenomena as they are “given to us” (i.e., in the phenomenological sense). The more we play with what’s in front of us, the more we’ll learn about what’s in front of us. Just staring at any given phenomenon or set of phenomena (even with the benefit of theory) won’t supply us with much when compared to our manipulations of nature.
This is, after all, what scientific tests and experiments are all about. Thus science has never been simply about observing and the mindless cataloguing of all the phenomena of nature. Not only do we demand answers from nature by asking it specific questions; we often only get those answers by playing with nature — that is, by experimenting on it and testing it. Observation alone can’t come up with answers. Not even observations alongside theory and a set of assumptions can come up with all the answers we want. Only experimentation, testing and other kinds of manipulation of nature will give us all that we want from nature — at least as far as physics is concerned.
Final Thought: Quantum Boxes aren’t Classical Boxes
One reason why a quantum box isn’t the same as a classical box is that in the case of the latter, there are no relevant (as such) disturbances from the outside. When it comes to classical boxes, what concerns the experimenter are anomalous differences, conditions and disturbances within the box, not outside it.
Despite that, there can still be obvious disturbances from the outside of a classical box — such as a gust of wind! (This would clearly effect the ball-on-an-inclined-plane experiment.) However, that wouldn’t be (or have been) problematic because it would have been very easy for the classical physicist or experimenter to factor it out
Yet in reality there are other outside disturbances or interactions which affect classical boxes. Indeed they’re the very same disturbances from outside which Smolin emphasises in the quantum-box cases. However, in the case of classical physics, these quantum or gravitational disturbances don’t make a difference to the classical scheme or to classical experiments.









No comments:
Post a Comment