An Account of Inductive Logic and Deductive Logic in the Late 19th Century

The 19th Century (ostensible) split between inductive logic and deductive logic.

In the second half of the 19th century many philosophers and (less so) logicians studied the kind of reasoning that’s employed in the experimental sciences. That basically meant that logic wasn’t really seen — by them — as being an autonomous discipline. In other words, they believed that logic was something developed by studying actual examples of reasoning.

There was a reaction against this historical and philosophical trend — if not always a conscious one. That reaction gave rise to mathematical logic and the new —and more rigorous — kinds of deductive logic of the early 20th century. That said, symbolic logic — from the mid-19th century onward — also existed alongside these other trends. In addition, mathematical logic can be dated back to George Boole’s works; some of which were written before the second half of the 19th century.

Inductive Inference and Soundness

What was the classic take on inductive inference?

It was that firstly people observe a finite amount of a given phenomenon. And then they generalise about such a phenomenon. The actual inference itself, therefore, is to as-yet-unobserved phenomena which will — or are hoped to — display the generalised features made about the observed phenomenon or phenomena.

For example, people infer (or did infer) that the next swan they’ll see will be white because they’ve seen many (or only) white swans.

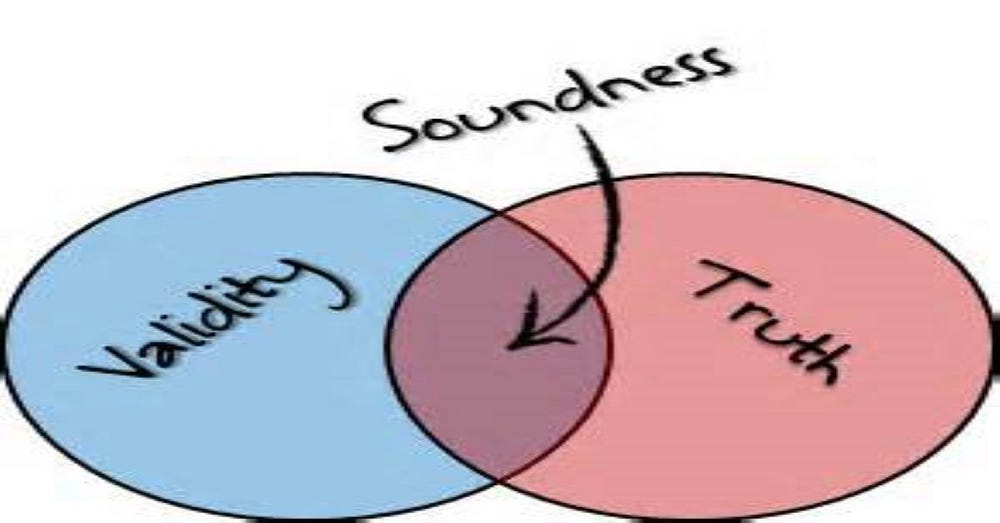
Now there’s an important difference between inductive inference and deductive inference. Inductive inferences aren’t sound; though (correct) deductive inferences are sound.

So what does the word soundness mean?

Firstly, soundness refers to a property of mathematical and logical systems; whereas an individual inference, statement or conclusion is said to be sound.

A sound inference or conclusion is an inference or conclusion which can’t be false given true premises. This means that a purely deductive inference must be sound. However, inductive inferences aren’t sound. Instead, inductive inferences are probable rather than sound. (It can’t be said that inductive logic is entirely about probabilities. See inductive probability.) So, in a strong sense, with inductive inferences we never have enough knowledge to fully warrant our conclusions. And that’s because no amount of knowledge would render the conclusions sound. Or, as the Dutch computer scientist and Professor of Artificial Intelligence Peter A. Flach puts it (in his ‘Modern Logic and its Role in the Study of Logic’), in inductive reasonings there will always be “missing knowledge”. Thus we must — instead — make “educated guesses” as to the nature of that missing knowledge.

Yet that lack of soundness wasn’t seen as being a big problem by many late-19th century philosophers; especially since soundness isn’t available — even in principle — when it comes to inductive logic. In fact, non-sound logic was still seen as being very useful. And, conversely, sound (deductive) logic was seen as being… well, pretty useless — at least at specific times or in particular situations.

There is a drawback.

That drawback is is that unsound conclusions may turn out to be (outright) false. Yet even this possibility isn’t so bad when seen in the light of, say, C.S. Peirce’s position of fallibilism. In other words, when we adopt this position we accept our own fallibility at the same time as being aware that we’re still making scientific, logical and philosophical progress.

Inductive Logic as the Logic of Truth

Many late-19th-century logicians and philosophers asked themselves the following question:

What truly distinguishes inductive logic from deductive logic?

The answer usually was that inductive logic is a “logic of truth”. Deductive logic, on the other hand, primarily deals with consistency, validity, consequence, soundness, etc. — all of which can exist in perfect isolation from truth. For example, a madman may be a fine deductive logician with a perfectly consistent and coherent world-view. Yet his world-view may well be based on things which are, nonetheless, entirely… false.

More technically, deductive logic can begin with premises which are simply false — and even known to be false! Yet that which is derived from such false premises may still be (internally) valid and consistent.

So why can’t we also say that whereas the premises are false, the deductions or inferences themselves are still true because they’re correctly derived from the premises?

Truth and Correctness in Logic

If the metaphysical notion of truth is so problematic and disparate, then why shouldn’t we call statements that belong to a valid and consistent system true? (Mathematicians do.) Yet all this will entirely depend on what, precisely, we take truth to be.

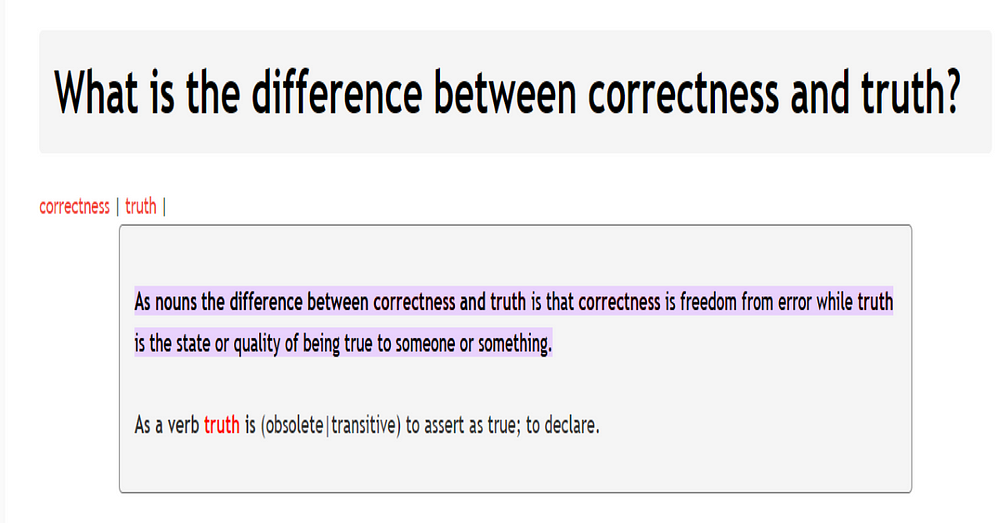
So the distinction between the words “correct” and “true” may be helpful here.

For example, we can say that a correct statement is a particular type of true statement. Alternatively, we can say that a true statement is a particular kind of correct statement. (These may be differences which don’t really make a difference.) In any case, some truths are determined by empirical realities. Whereas other truths are determined by the fact that they’re correctly derived (or deduced) from given premises, statements or axioms.

Much the same was the case with Ludwig Wittgenstein’s distinctions between statements which are true and statements which are (merely?) correct (see here). More specifically, Wittgenstein believed that certain things are deemed true simply because they conform to conventions, rules and/or norms. (He even applied this position to the “truths” of mathematics.) On the other hand, many people deem other things to be true in spite of what the community thinks or regardless of conventions, norms or rules.

So why not simply invert these terms in that “truth” becomes “correctness” and “correctness” become “truth”? The point here is that although these distinctions are effective in distinguishing certain types of statements from one another, they’re rarely distinguished from the perspective of metaphysically analysing the nature of truth itself.

So are these distinctions just ones of use and convenience? In other words, do they have any metaphysical or even semantic weight?

Deductive and Mathematical Logic

Perhaps mathematical logic all began with George Boole (1815–1864). The book above was published in 1847.

Much of early-20th-century logic developed in isolation from science and everyday reasoning. (Of course it was still believed that such a logic’s findings could — or would — be applicable outside the logic itself.) In simple and broad terms, it can be argued that logic also became less relevant to other areas of discourse in the early 20th century. More specifically, it became less relevant to philosophy and to the experimental sciences.

The simple reason why deductive logic impressed 20th century mathematical logicians and philosophers (see mathematical logic) is that in any deductive system one “moves from truths to further truths”. In inductive logic, on the other hand, one moves from probabilities to further probabilities. Thus inductive logic isn’t airtight in the manner in which deductive logic is. In the latter case, one essentially accumulates more truth (if “truth” is the correct word here) from a given set of truths (e.g., from premises, axioms, etc.).

Why, exactly, were non-deductive forms of reasoning largely ignored in the Fregean (see here) and post-Fregean age of mathematical logic? The answer is that they could provide no help to what’s often been called “foundational research” in mathematics. (See the foundations of mathematics.) And, of course, mathematical systems are often (or always) deductive systems. (Even “mathematical induction” is deemed to be deductive!)

Indeed all this was part and parcel of the rejection of any form of (what was called) psychologism in logic, mathematics and philosophy.

“Pure logic” (to use Edmund Husserl’s term) doesn’t deal with thought processes at all. It is (or was) believed — by many — to deal with timeless logical laws, truths and principles which — arguably — would exist even if no one had thought about (or expressed) them. Inductive reasoning, on the other hand, fundamentally relies on observations. Thus the notion of observation is clearly a psychological one. And the same goes for (to cite a more specific example) C.S. Peirce’s theory of abduction. (Here the abductive act is a psychological phenomenon - even a creative one.)

As hinted at earlier, people don’t really rely that much on deductive logic in their everyday lives. More clearly, both mathematical logic and deductive logic don’t seem to be closely connected to how people actually reason. Now that may be simply be because most people don’t reason correctly. (Consequently, perhaps they should mimic the inferences of deductive logic and mathematical logic.) On the hand, inductive logic is primarily concerned with observations and inferences from those observations.

Consequently, all the words above may make it seem strange that mathematical logic was so important to so many (analytic) philosophers of the first half of the 20th century.

******************************

Note: A Short Digression on C.S. Peirce’s Theory of Abduction

C.S. Peirce’s notion of abduction may seem, at least prima facie, to be indistinguishable from induction.

An abduction somehow explains certain observations. In other words, it’s a hypothesis. Or, the other way around, from such an abductive hypothesis we can know what kind of observations to expect given pre-existing data. However, unlike induction, an abductive argument will begin with some kind of generalisation. Thus:

i) All the beans from this bag are white.

ii) These beans are white.

iii) Therefore, these beans are from this bag.

The second premise moves to the particular. The conclusion, in this case, in a sense fuses the first and second premises. That is, because all the beans in the bag are white, then it’s probable that these particular white beans may be from that bag. In the above example, it’s not yet known where the white beans have come from. The conclusion, given in the first premise, hypothesises the probability that given all the beans in the bag are white, then these particular white beans may be — or are — also be from the bag.

Indeed the first premise (“All the beans from this bag are white”) can itself be seen as the conclusion of a previous inductive argument. That is, from the observations of many particular white beans, it might have been concluded that all the beans in the bag must be white. Or, to use Peter Flach’s terms again, the first premise of the abductive argument gives us the inductive “general rule”. The abductive part of the argument will be the inference that the particular white beans in front of the observer are probably from the bag of white beans. In this instance, abduction takes over where induction left off.

[I can be found on Twitter here.]