First things first.
The following essay isn’t going to tackle Bertrand Russell’s famous (or infamous) paradox (i.e., Russell’s Paradox). Instead, it’s going to deal with some of the set-theoretical and philosophical details which led up to the paradox. Primarily, it asks various questions about the philosophical (i.e., ontological) nature of sets. Specifically, questions about the Universal Set — or the Set of Everything.
******************************

Rather bizarrely, the English philosopher Bertrand Russell (1872–1970) once set out to calculate how many things there are in the universe. And after Russell had done that, he was led to conclude that there must (or simply could) be a set which includes literally everything (or every… thing).
(Of course the practical problems with such an act of “counting” are irrelevant because this was a purely mathematical or set-theoretical enterprise.)
This set came to be called the Universal Set. And that set, in turn, led to a well-known paradox — Russell’s Paradox.

Russell originally reasoned in this rather odd way in order to counteract Georg Cantor’s view that there is no largest number. Russell himself said — when looking back in 1919 — that he’d “attempted to discover some flaw in Cantor’s proof that there is no greatest cardinal”.
Russell claimed that if he could (as it were) discover a set which included literally every… thing, and that the nature of sets determines the nature of numbers (or that sets literally are numbers), then that set would be the largest number.
In short and on the resultant paradox.
In the 1890s Georg Cantor himself had already come to realise that his positions on sets would lead to a contradiction. Indeed he communicated this finding to David Hilbert (1862- 1943) and Richard Dedekind (1831–1916). That said, Cantor didn’t technically formulate the paradox: Ernst Zermelo (1871–1953) did. Moreover, in 1903 Hilbert (again) wrote a letter to Gottlob Frege (1848–1925) about Russell’s paradox in which he wrote the following words: “I believe Dr. Zermelo discovered it three or four years ago.” However, Zermelo (like Cantor before him) never published his finding.
Sets and Numbers
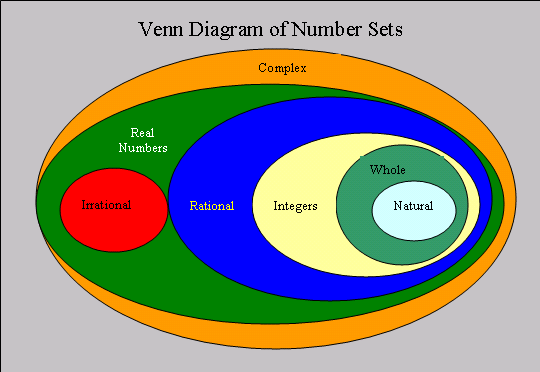
Clearly with Russell’s (early) position we have the notion that the members of a set determine that set. And, if that’s the case, then there must be a largest number — at least if we follow Russell’s reasoning at that point in his career. (In set theory, the actual nature of numbers and sets is much disputed — see later.)
According to Russell and Frege before him, numbers are sets. Therefore what makes up a set determines or (as it were) constitutes a number. So if literally everything (or every thing) is included in a set, and that set is finite, then it also determines the finitely largest number.
But what did Russell mean by the word “everything”? Did he mean only every concrete or empirical thing? What about minds? Indeed what about abstract entities such as universals, properties, possible worlds… and numbers? Yet if Russell had included abstract objects (or entities) in his (to use German/Platonic capitals) Set of Everything, then surely it couldn’t have included everything because numbers, for one, are infinite…
Of course that statement raises two issues:
(1) If sets determine (or constitute) numbers, then numbers clearly can’t be the members of sets.
(2) Is there an assumption (from the outset) here that there are (or are not) actual infinities?
As just hinted at, one can’t call in numbers here because it’s the nature of sets (at least in this theory) which determines the nature — and even existence — of numbers.
More simply, that Set of Everything can’t have numbers as members because sets themselves are deemed to be numbers.
But are Numbers Really Sets?

The problematic nature of (in the singular) set theory is displayed by statements such as the following:
“Many set theories do not allow for the existence of a universal set.”
Yet some set theories do allow for the existence of a universal set.
This multiplicity of set theories hints at either the complexity of the issue or that there’ll never be a definitive (or conclusive) position on the nature (rather than the mathematical everyday use) of sets and numbers. And perhaps the main reason for this is one of the following: 1) Sets are abstract. 2) Sets (at least if seen as Platonic entities) don’t exist at all.
So are these essentially philosophical — even stipulative — interpretations of sets and numbers simply vying for intellectual dominance?
In any case, if numbers are sets, then sets are numbers. Thus:
If sets = (i.e., are numerically identical to) numbers, then numbers = sets
Yet the often-seen phrase “sets of a number” (or “sets of numbers”) implies, by its very grammar, that sets can’t be (or equal) numbers. Specifically, the two words “sets of” implies that there are sets and there are numbers. (Alternatively, there is a set and there are that set’s members.) The same kind of reasoning also applies to phrases such as “numbers are represented — or modelled - by sets” and “the natural numbers can be constructed using sets”.
So some theorists argue that there are sets and there are the sets’ members. The two are very different. Analogically, there is a collection of sweets and the bag that the sweets come in. Clearly the bag and the sweets aren’t identical. Thus saying “There is no bag of sweets” (i.e., there is no set) and saying “The bag of sweets is empty” (i.e., the set is empty) are two very different statements.
Yet because we’re talking about abstracta here (i.e., sets and numbers, not bags and sweets), then that analogy may well break down.
In any case, any given x can’t also be y. Of course that’s only if the symbols x and y symbolise (or refer to) physical or abstract objects, not intensional terms, the content of psychological states… or, for that matter, sets. (Intensions basically “belong” to words/terms or psychological states, not to things. However, that’s the case even though such words or psychological states can actually be “about” things.)
As for sets. Jimmy the cat (x) belongs to the set of mammals (y). Yet if we’re talking about individual objects and not sets, Jimmy the cat can’t actually also be Johnny the dog — which is also a mammal (x ≠ y).
On the other hand, many (or even all) the arguments which state that numbers aren’t sets rely on the (Platonic) position that numbers are (eternal) abstract objects. That said, sets too are usually seen to be abstract in nature. That said, Bertrand Russell (again) once believed that all a set’s members (when taken together) literally constitute — or are — the said set. Yet it’s unclear if Russell’s view — even if true or correct — automatically stops sets from being abstract.
There’s also problems with the empty set (symbolised: {}) and sets which only have one member. (A set with one member is called a singleton or unit set -sometimes symbolised: { s }.) In the case of the empty set, there’s literally nothing (or no thing) to determine the nature of that set. And in the case of sets with only one member (whose one member can even be {null}), then such sets and “their” single members (or elements) must be one and the same thing.
So why the need to postulate such sets in the first place?
Conclusion

Finally, it can be said (if only in very broad terms) that mathematics works fine as it is: it’s only the philosophical nature of numbers and sets that’s problematic. Indeed this parallels — at least to some extent - the clear opposition between the mathematical formalism/s of quantum mechanics and the many and various interpretations of that theory.
To repeat: mathematics is a domain of much consensus. Yet the domain of the philosophy of sets and numbers isn’t. Indeed there are (to be melodramatic for a moment) an infinite amount of actual and possible positions to take on the ontological nature of sets and numbers.











No comments:
Post a Comment