Everyone who knows anything about the mathematical physicist, theoretical physicist and mathematician Roger Penrose (1931-) knows that he’s a mathematical Platonist.
What may also be relevant (to this discussion) is the fact that Penrose also speaks (if indirectly) about Plato’s position on the transmigration (or metempsychosis) of the human soul! (The words “transmigration” and “metempsychosis” aren’t, of course, used by either Plato or by Penrose.)
Specifically, readers may wonder how and why (some) mathematicians (to use Penrose’s oft-used word) “see” mathematical truths — specifically of the Gödelian kind. Penrose himself provides an answer to that. And his answer includes an indirect reference to Plato’s theory of transmigration.Penrose firstly explains the very particular nature of mathematical truths. He writes:
“Because of the fact that mathematical truths are necessary truths, no actual ‘information’, in the technical sense, passes to the discoverer.”
So far so good.
Yet then we get what must be a (if there is such a word) transmigrational reason for this. Penrose continues:
“All the information was there all the time. It was just a matter of putting things together and ‘seeing’ the answer! This is very much in accordance with Plato’s own idea that (say mathematical) discovery is just a form of remembering!”
Penrose uses the word “information” in the same way that many physicists use it. In other words, it’s certainly not a word used by mathematicians in their everyday work. This means that if we aren’t dealing with information (i.e., in the physicist’s sense) when it comes to mathematical truths, then another way of accounting for such truth must be found.
[It’s not immediately clear how the “fact” that mathematical truths are also “necessary truths” glides over into Platonic seeing. Penrose must mean that, in a simple sense, necessity can never be seen, observed, or experimented upon — it must be “found” by insight or by Platonic seeing. Indeed most metaphysicians — if only the ones who accept it — would agree that necessity isn’t an “observable property”.]
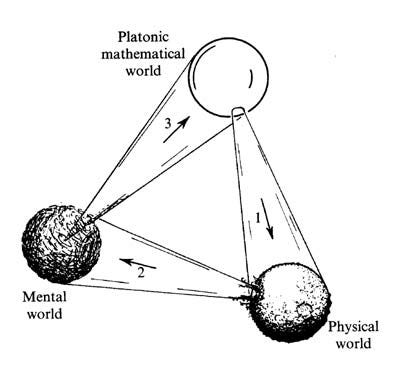
As for Platonic transmigration specifically.
The word “transmigration” is used because Plato is widely thought to have believed in the transmigration of the human soul from one body to another. Thus when Penrose uses the word “remembering”, what that actually means — within this context — is that a mathematician alive today must remember what his “soul” saw when it existed in another body in a “previous life”. Perhaps more accurately, the mathematician alive today — or even Penrose himself! — literally remembers his previous access to mathematical truths.
(It must be said here that some commentators — such as philosophers dating back to the Catholic priest and scholar Marsilio Ficino (1433–1499) — argue that Plato’s references to transmigration — or to metempsychosis — were intended to be allegorical in nature. This isn’t a surprise since this interpretation of Plato’s philosophy has mainly come from Christian thinkers.)
Of course, this introduction of past selves (or past souls) doesn’t tell us how such beings themselves gained access to mathematical truths either!
More specifically on Penrose’s broader position on algorithms and consciousness: it’s probably best to allow Penrose himself to put it all in some kind of context. Here goes:
“Great works of art are indeed ‘closer to God’ than are the lesser ones. It is a feeling not uncommon amongst artists, that in their greatest works they are revealing eternal truths which have some kind of prior etherial existence I cannot help feeling that, with mathematics, the case for believing in some kind of etherial, eternal existence is a good deal stronger than in those other cases [such as art and engineering].”
Then Penrose (elsewhere) moves away from Platonic truth and toward the subjects of “awareness” (or consciousness) and “substance”. He writes the following:
“Perhaps, on the other hand, there is more to our feelings of awareness than mere algorithms. Perhaps the detailed way in which we are constituted is indeed of relevance, as are the precise physical laws that actually govern the substance of which we are composed.”
Penrose on Gödelian Truth

The first thing to say is that if there is such a thing as mathematical truth (rather than mathematical correctness, formal consistency, etc.), then it must be very different from other kinds of truth. (Take these examples: truth as cashed out in terms of correspondence, coherence, “the word of God”, pragmatic utility, etc.) Roger Penrose himself acknowledges this. Basically, he believes that mathematical truth is Platonic. This means that Penrose has little time for naysayers when it comes to mathematical (therefore Platonic) truth. He makes that clear in the following passage:
“As to the very dogmatic Gödel-immune formalist who claims not even to recognize that there is such a thing as mathematical truth, I shall simply ignore him, since he apparently does not possess the truth-divining quality that the discussion is all about!”
[Note the word “divining”.]
In basic terms, mathematical truth — on Penrose’s definition — is exterior to all algorithms.
So what exactly does Penrose mean by “truth” in these contexts?
Penrose seems to assume that truth is part of (all?) mathematical systems when he says such things as “whatever formal system [a mathematician] might adopt as proving his criterion of truth”. In other words, not much more is said here — or indeed elsewhere — about what mathematical truth actually is. Then again, Penrose’s Platonic truth may be so brute (or fundamental) that nothing much can be said about it. (When a mathematician sees mathematical truth, is this an example of what the philosopher Paul Boghossian calls “flash grasping”? See also brute fact.)
Penrose explains what he takes to be the chasm which exists between algorithms and consciousness (primarily viewed in terms of Gödel’s first incompleteness theorem) in the following passage:
“[T]he very essence of consciousness. It must be present whenever we directly perceive mathematical truth. When we convince ourselves of the validity of Gödel's theorem we not only ‘see’ it, but by so doing we reveal the very non-algorithmic nature of the ‘seeing’ process itself.”
The words above state an explicit and essential link between consciousness and the ascertaining of mathematical truth. Basically, consciousness is required to (using Penrose’s word) “see” mathematical truth. (Penrose repeatedly puts the word see in scare quotes — i.e., he doesn’t mean literal seeing through the eyes.) This also means— to Penrose at least — that mathematical truths can’t be seen by computers or machines. Yet that’s not because computerised robots or even rudimentary computers have no (non-biological) eyes or visual systems (some would argue that they do) — but because they have no consciousness.
So, unlike that artificial intelligence (AI) theorists (at least according to Penrose himself), not only is it impossible for algorithms alone to bring about (or even simulate) consciousness, consciousness actually predates both the human construction and the human use of algorithms (if not also their actual abstract existence — see the final section on AI). This means that if conscious human beings can do at least one thing (such as see mathematical truths) which the use — and existence — of algorithms alone will never allow us to do, then consciousness must be above and beyond algorithms. In other words, that which is above and beyond algorithms can’t also be brought about — or simulated — by algorithms.
Penrose (elsewhere) also wrote:
“[C]oncerning Gödel's theorem, was that, at least in mathematics, conscious contemplation can sometimes enable one to ascertain the truth of a statement in a way that no algorithm could.”
Basically, the ascertaining of (Gödelian) truths is non-algorithmic. Thus — again — algorithms cannot bring about (or simulate) consciousness. Or, at the very least, algorithms cannot bring about (or simulate) the type of consciousness which is required to ascertain Gödelian truths.
Indeed not only is all this the case when it comes to Penrose’s position on consciousness, he even takes this position on (“genuine”) intelligence too. (As shall be seen in the final section.)
Penrose on Algorithms and Judgements About Algorithms
Penrose offers us a personal — and seemingly obvious — distinction between consciousness and using algorithms. Or, more precisely, he makes a distinction between consciousness and the conscious process of using (or performing) algorithms.
At first sight, however, it may seem that Penrose is simply assuming that
“the decision as to the validity of an algorithm is not itself an algorithmic process!”.
In other words, it can’t be seen in any of Penrose’s surrounding arguments why that must be the case. Unless that is, he simply means that, say, algorithm A can’t decide “the validity of”… algorithm A.
In any case, one can agree with Penrose and argue that in the conscious act of using (or performing) an algorithm there’s still a distinction which can be made between that algorithm itself and the conscious state/s in which that use (or performance) is (as it were) embedded.
Penrose goes into detail here and stresses consciousness.
He firstly asks this question:
“Why do I say that the hallmark of consciousness is a non-algorithmic forming of judgements?”
Penrose answers his own question by making an obvious(?) distinction between algorithms-in-the-brain and (as it were) algorithms-in-awareness. He continues:
“Part of the reason comes from my experience as a mathematician. I simply do not trust my unconscious algorithmic actions when they are inadequately paid attention to by my awareness.”
Basically, Penrose is arguing that we mustn’t confuse (or conflate) the algorithms which occur in the brain (i.e., the ones which AI theorists often focus on) and how these algorithms manifest themselves in what Penrose calls “awareness”.
So Penrose clearly doesn’t deny the algorithmic nature of many (or even all?) brain processes. (Penrose may well have changed his mind on this — it’s hard to say.) The following is what he says on that matter:
“My own line of reasoning has been that unconscious processes could well be algorithmic, but at a very complicated level that is monstrously difficult to disentangle in detail.”
What’s more:
“The fully conscious thinking that can be rationalized as something entirely logical can again (often) be formalized as something algorithmic [].”
That’s all fine as it stands.
However, what Penrose wants to stress is at an “entirely different level”. He continues:
“We are not now thinking of the internal workings (firings of neurons, etc.) but of manipulating entire thoughts.”
Penrose then concedes that “[s]ometimes this thought-manipulation [also] has an algorithmic character”. However, “sometimes it has not”. (He gives the example of seeing the truth of a Gödel sentence.)
Basically put, then, algorithms themselves simply don’t equal what happens when we consciously use those algorithms.
Penrose then makes another (obvious?) distinction between an algorithm itself and the conscious processes which are above and beyond the use of that algorithm. This is a clear hint at what differentiates human beings (or persons) from computers or machines. He continues:
“Often there is nothing wrong with the algorithm as an algorithm, in some calculation that is being performed, but is it the right algorithm to choose, for the problem in hand?”
Penrose (elsewhere) adds the following:
“Moreover the mathematical judgement that some algorithm is indeed accurate or appropriate is the sort of thing that requires much conscious attention.”
It’s not clear that Penrose’s distinction directly above is as strong as his previous ones. After all, it’s (fairly) obvious that an algorithm must be chosen and that choice comes before the use of the algorithm itself. That conscious choice isn’t — therefore — equal to the algorithm. More clearly, the conscious processes used to select an algorithm can’t be a product of the algorithm that’s chosen.
Yet it can still be argued that once the algorithm is chosen — and then performed (or used) — there’s nothing over and above that performance (or use). That is, there isn’t an extra insightful glow provided by consciousness itself. So even if there is a distinction between an algorithm as it is in itself (or even as it is in the brain) and the conscious awareness of that algorithm when performed (or used) by a conscious person, that something extra may not provide us with anything extra special or Gödelian.
Penrose then makes the same (or at least a similar) point in the following passage:
“One often strives for algorithms, when one does mathematics, but the striving itself does not seem to be an algorithmic procedure.”
This again seems like a statement of the obvious because surely no one would ever argue that this “striving” is itself algorithmic…. Or at least it must be said that the algorithms involved in the striving aren’t the same ones that are “found” as a result of that striving. Yet what if that that striving itself does indeed include the use (or performance) of different algorithms? That is, the use (or performance) of algorithms may lead to the discovery of other algorithms.
To repeat.
Stating that “the decision as to the validity of an algorithm is not an algorithmic process” doesn’t mean that another algorithm (or algorithms) can’t be used to decide on the validity of the algorithm under scrutiny. So this isn’t circular reasoning if two — or more — different algorithms are employed.
The same can be said about Penrose’s claim that
“[i]n order to decide whether or not an algorithm will actually work, one needs insights, not just another algorithm”.
… Except that here Penrose squashes my previous point about using other algorithms to scrutinise a given algorithm.
In any case, what are these “insights”? And why can’t such insights (whatever they are) be strongly connected to algorithms — or even be algorithmic?
Now all the above was Penrose on what comes before the discovery of an algorithm. However, Penrose also has something to say about when a mathematician is working with a mathematical system of axioms, theorems and algorithmic rules. And here again he tells us that there’s still something above and beyond the system itself.
Penrose on Systems and Judgements About Systems
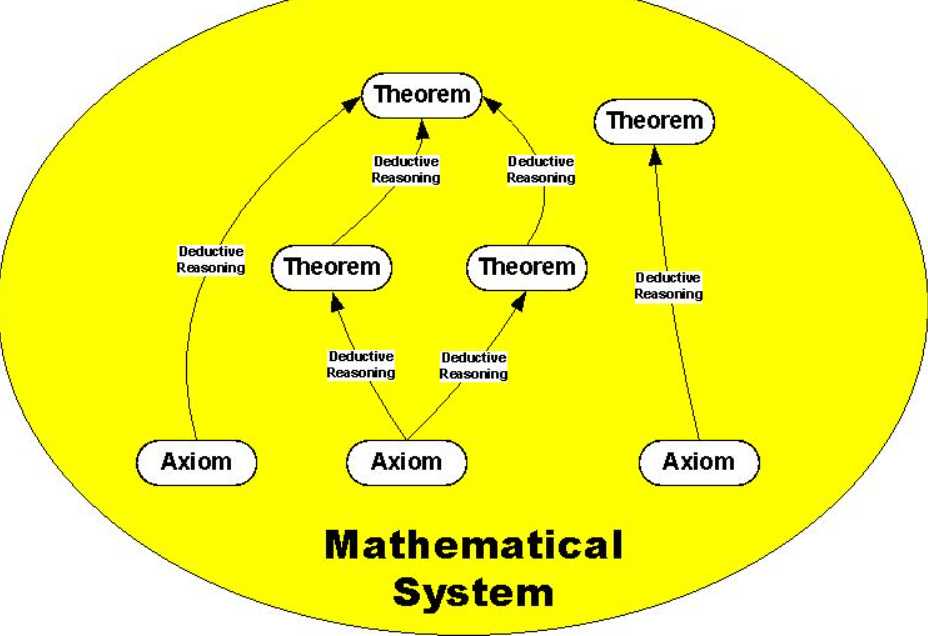
Firstly, a few words of warning.
In the following nothing detailed is going to be said about Gödel's theorems in themselves. That’s mainly because this is an issue which has already been extensively — very extensively! — covered. That said, it’s worth stating Penrose’s succinct encapsulation of Gödel's first incompleteness theorem (to get it out of the way) within this very discussion of the limitations (or not) of algorithms.
Penrose writes:
“If the workings of the mathematician’s mind are entirely algorithmic, then the algorithm (or formal system) that he actually uses to form his judgments is not capable of dealing with the proposition Pₖ(k), constructed from his personal algorithm. Nevertheless, we can (in principle) see that Pₖ(k) is actually true!”
So the following words aren’t an attempt to question the “validity of the Gödel proposition Pₖ(k)”. In other words, one can accept that we “cannot derive it from the axioms” of any given mathematical system. The point being made is about how far and wide Penrose and others seem to stretch things — that is, way beyond the inability to “see the truth” of Pₖ(k) from within the mathematical system in which it is embedded. Indeed even most (or all) mathematicians and philosophers who’re inclined to formalism accept this Gödelian (as it were) fact. What they don’t accept is the stretching and widening of Gödel's first theorem way beyond mathematical systems — to such things as truth in general, systems in general, consciousness and (sometimes) everything else under the sun!
So what does Penrose himself have to say on these matters?
Penrose firstly links his Gödelian (or Platonic) position on an individual algorithm to his position on an individual mathematical system. He sees that both generate exactly the same problem for “formalists” and others.
Penrose writes:
“[W]e shall need to employ insights from outside the system — just as we did in order to see that Pₖ(k) was a true proposition in the first place. It s these insights that cannot be systematized — and, indeed, must lie outside any algorithmic actions!”
Of course, Penrose accepts the utility of algorithms within any given mathematical system. He puts it this way:
“One may start with some axioms, from which are to be derived various mathematical propositions. The latter procedures may indeed by algorithmic [].”
And then Penrose follows with a “but”. He continues:
“[B]ut some judgement needs to be made by a conscious mathematician to decide whether the axioms are appropriate. That these judgements are necessarily not algorithmic [].”
Again it can be said that the judgments as to “whether the axioms are appropriate” may also be algorithmic. Yet Penrose argues that “these judgments are necessarily not algorithmic”.
So why is that?
Penrose tells us that “we shall need to employ insights from outside the system”. Yet — again — these “insights” may well be algorithmic too. In fact, even when it comes to Gödel sentences (or truths), this is accepted by many commentators. Penrose himself denies this and cites the case of seeing the truth of Pₖ(k) and that “must lie outside any algorithmic action!”.
As already hinted at, it’s widely accepted that the truth of any given Pₖ(k) cannot be established from within the system it belongs to. Yet why can’t an algorithm on the outside of the system do that job instead?
Penrose’s own stance on this is that he believes that we have a (kind of) nesting problem (or situation) here in that any algorithm on the outside of the system would itself encounter the same Gödelian impasse. Yet surely this wouldn’t be a problem of not being able to use exterior algorithms to the given system, but one of a possible(?) infinity(?) of new Gödel sentences.
Penrose hints at this problem — or at least a similar one — when he tells us that this
“putative ‘universal’ system, or algorithm, cannot ever be known as the one that we mathematicians use to decide truth!”.
And then Penrose explicitly states the nesting problem by concluding with these words:
“For, if it were, then we could construct its Gödel proposition and know that to be a mathematical truth also.”
In addition, Penrose writes:
“Accordingly, we adjoin G₁ to our system also. This gives us a further amended system which will have its own Gödel proposition G₂ (again perfectly valid), and we can then adjoin this, obtaining the next Gödel proposition G₃, which we also adjoin, and so on, repeating this process indefinitely. What about the resulting system when we allow ourselves the entire list G₀, G₁, G₂, G₃,… as additional axioms? Might it be that this list is complete?”
To put in very simple terms: no matter what we add to our mathematical system, a new Gödel sentence (or truth) will arise. And the truth of that Gödel sentence can only be discovered via Platonic insight, not by the use of yet another algorithm.
To broadly comment — critically — on Penrose’s position as just expressed.
No one — not even a person Penrose (dismissively) calls “formalist” — would ever deny that there are elements of reasoning, judgments, thinking, etc. outside the system which the mathematician is presently dealing with. No one needs to be an across-the-board Gödelian to realise and accept that. So that means that we can indeed also “leap outside the rigid confinements of any formal system” to reason, think, etc. about the said system.
Yet should we draw all the same conclusions as Penrose himself does about all this?
Do these Gödelian realities about mathematical(!) systems really have the deep and wide implications which Penrose and so many others are so keen on stressing?
Penrose on Algorithms, Turing and Artificial Intelligence

Roger Penrose — as is almost inevitable within this context — mentions Alan Turing (1912–1954). In Penrose’s own words:
“Alan Turing (1950), in his famous paper, did not refer so much directly to ‘consciousness’, but to ‘thinking’, and the word ‘intelligence’ was in the title. In my own way of looking at things, the question of intelligence is a subsidiary one to that of consciousness.”
Then comes a fundamentally important statement from Penrose. He continues:
“I do not think that I would believe that true intelligence could be actually present unless accompanied by consciousness.”
A few moments later, Penrose adds the following words:
“When I assert my own belief that true intelligence requires consciousness, I am implicitly suggesting (since I do not believe the strong-AI contention that the mere enaction of an algorithm would evoke consciousness) that intelligence cannot be properly simulated by algorithmic means, i.e. by a computer, in the sense that we use that term today.”
On the surface at least, this is an incredible and perhaps extreme claim. That’s said because most commentators accept that no computer is conscious and that algorithms alone may not be enough for consciousness. Yet Penrose is going one giant step beyond all that and saying that algorithms aren’t even enough to bring about (what he keeps calling) “true intelligence” either!
AI Platonists?

Interestingly, Penrose seems to argue (or he does argue) that AI theorists are actually closet (or disguised) Platonists anyway — at least when it comes to algorithms. Their sin is the (as it were) reification of abstract algorithms. This is how Penrose himself puts it:
“But for an algorithm to ‘exist’ independently of any particular embodiment, a Platonic viewpoint of mathematics would seem to be essential.”
That certainly seems like a convincing argument. After all, AI theorists repeatedly stress the abstract nature of algorithms. That is, they stress the fact that the same algorithm can be embodied in all sorts of very different physical substrates. Thus just as many philosophers argue that mental states, properties or events can be what they call “multiply realised”, so too can algorithms.
[The American philosopher John Searle similarly accuses strong-AI theorists of algorithm-brain dualism. As an example of this, Searle once stated the following: “[S]trong AI only makes sense given the dualistic assumption that, where the mind is concerned, the brain doesn’t matter.”]
Penrose’s additional statement, however, isn’t so clear. He concludes:
“It would be difficult for a strong-AI supporter to take the alternative line that ‘mathematical concepts exist only in minds’, since this would be circular, requiring minds for the existence…”
It’s not clear what philosophical (or ontological) position most (or even any) “AI supporters” take on algorithms or on “mathematical concepts” generally. That said, Penrose’s own description paints AI theorists as mathematical Kantians or intuitionists (i.e., in their stress on minds alone). Yet Penrose’s final clause (i.e., “since that would be circular, requiring pre-existing minds for the existence…”) still seems a little odd.
Is the following Penrose’s argument? -
i) If — as AI theorists argue — algorithms (in the brain and elsewhere) literally bring about “minds”,
ii) then how can they “only exist” in minds”?
In other words, within this seemingly Kantian (or intuitionist) position, minds must firstly exist in order for any algorithms (or “mathematical concepts”) to exist — or even be constructed — within them. Yet AI theorists won’t — or can’t — accept that because they see algorithms (not human minds) as being primary. Consequently, AI theorists must implicitly uphold— if we accept Penrose’s argument — their own kind of mathematical Platonism.










No comments:
Post a Comment