Douglas Hofstadter’s simple reworking of Kurt Gödel's First Incompleteness Theorem.
Douglas Hofstadter (who was born in 1945) is an American mathematician, cognitive scientist and physicist who has written on artificial intelligence (AI) and consciousness. He’s primarily known for his book Gödel, Escher, Bach: An Eternal Golden Braid. This book won the Pulitzer Prize and a National Book Award for Science. It’s also the primary source of this essay.
Self-Reference is Everywhere

Douglas Hofstadter’s Gödel sentence G is almost entirely based on Kurt Gödel's very own G — as it’s displayed in the latter’s first incompleteness theorem. (Of course Gödel himself never used the symbol G or the words “Gödel sentence”.)
Hofstadter also picked up on the importance of self-reference when it comes to Gödel's G, mathematical systems and indeed metamathematics as a whole.
It can now be said that the entire enterprise of metamathematics can be seen to be self-referential. Indeed, according to Hofstadter himself, Gödel's main idea was
“to use mathematical reasoning in exploring mathematical reasoning itself”.
Hofstadter concluded by saying that
“perhaps its richest implication was the one Gödel found: Gödel's Incompleteness Theorem”.
In more particular terms and with more direct relevance to this essay, Hofstadter also told us that
“it is in the nature of any formalization of number theory that its metalanguage is embedded with it”.
In broad terms, then, Gödelian metamathematics was a kinda incestuous or nepotistic enterprise. (Analogically, it was a little like getting the police to investigate the police.) Yet this was seen to be a good thing by Gödel and by many others. That’s primarily because what better means of investigation (or analysis) can there be than using mathematics? So, if that’s the case, then why not use mathematics to analyse (or investigate) mathematics itself?
In addition and on a simpler scale: if numbers can code individual symbols and whole statements, then all sorts of juxtapositions (or even games) will be made possible. After all, numbers are the domain of the infinite. And this may also mean that Gödelian number coding will also be the domain of the infinite.
In any case, from maths being applied to maths, we had the consequence of Gödel's First Incompleteness Theorem — which itself introduced statements (or mere “strings”) which referred to themselves. More precisely, we then had self-referential symbols which were actually embedded within the statements they were about. And, in turn, such symbols and statements were assigned a number.
What is a Theorem?

Since the term “theorem” is central to this essay, let Douglas Hofstadter himself tell us what it is. Thus:
“Such strings, producible by the rules [within mathematical systems], are called theorems.”
Hofstadter then made a distinction between two types of theorem.
Firstly, he explained the first (“common”) type of theorem:
“The term ‘theorem’ has, of course, a common usage in mathematics which is quite different from this one. It means some statement in ordinary language which has been proven to be true by a rigorous argument, such as Zeno’s Theorem about the ‘unexistence’ of motion, or Euclid’s Theorem about the infinitude of primes.”
Then, more relevantly to this essay, Hofstadter defines the second type:
“But in formal systems, theorems need not be thought of as statements — they are merely strings of symbols. And instead of being proven, theorems are merely produced, as if by machine, according to certain typographical rules.”
The words “merely strings of symbols” strongly and perfectly explain much about self-referential paradoxes and indeed Hofstadter’s own G. That is, such theorems aren’t “thought of as statements” primarily because they contain no semantic content. (Arguably, the very fact that “empty” symbols and strings can be used and manipulated in specific and prescribed ways means that they must indeed have a semantics!) And, because of that, these theorems (such as G itself) “instead of being proven”, are “merely produced” (i.e., “as if by machine, according to typographical rules”).
Thus if these theorems are merely(?) strings of symbols, then no wonder we can play logical games with them. Like an actual material string, we can tie the theorems and symbols in a multitude of different “knots”. However, if symbols or logical strings were actually meant to mean something, or refer to something outside themselves, then perhaps such logical games wouldn’t be possible.
Douglas Hofstadter’s Sentence G

Douglas Hofstadter cites a (or even the) problem with self-reference — at least when it comes to self-referential sentences or what he calls “strings”. (It’s not clear — at least to me — if Hofstadter himself sees it as a problem.)
Hofstadter cites sentence G, which is a theorem of his own Typographical Number Theory (TNT).
So what is theorem G? This:
G is not a theorem.
Firstly: note that Hofstadter used both the words “if G were a theorem” and “[G] being a theorem”. This must mean that G both is and is not a theorem in Hofstadter’s Typographical Number Theory.
Hofstadter also stated that
“if G were a theorem[of Typographical Number Theory] , it would express a truth”.
G would state a truth because, according to Hofstadter, “TNT never has falsities for theorems”.
So the sentence (or what Hofstadter calls a “string”)
G is not a theorem.
must be “a truth”.
G says of itself that it’s not a theorem and that statement is also (taken to be) true.
Yet G is also a theorem (as in Hofstadter’s “[G] being a theorem”) of TNT!
For comparison: in one formal expression of the Liar Paradox, the statement “(A) Statement A is false” turns out to be both false and true. In Hofstadter’s case, on the other hand, G turns out to be both a theorem and not a theorem. And, of course, Hofstadter’s own G also involves the notion (or property) of truth.
Hofstadter put all the above in another way by stating the following:
“By being a theorem, G would have to be a falsity.”
Why is that? Because (again) G says of itself:
G is not a theorem.
And if G is not a theorem, then what status does it have? Hofstadter has already told us that all theorems of TNT must be true. So G is true because it’s a theorem of TNT. Yet it’s also a theorem which states — of itself — that it isn’t a theorem. Basically, then, G must be true in a way that that’s at odds with what Hofstadter calls “common” theorems. And G is so in the sense that it’s true at the same time as saying it isn’t a theorem. Moreover, G’s truth cannot (therefore) be proven within TNT.
So does that also mean that G (as it were) becomes a theorem of TNT by virtue of it saying (of itself) that it “is not a theorem”? That is, by denying its own theoremhood, does G becomes a theorem? Thus “G is not a theorem” must also be true in order for it to be a theorem. Yet, because G says (of itself) that it “is not a theorem”, then that must mean that it is (or at least can be) a theorem of TNT. Thus G’s saying of itself that it isn’t a theorem is also a statement of its (or a) truth. And, by denying its own status as a theorem, G actually becomes a theorem.
Now let’s spend a little time on Gödel's own G.
Kurt Gödel’s Own G
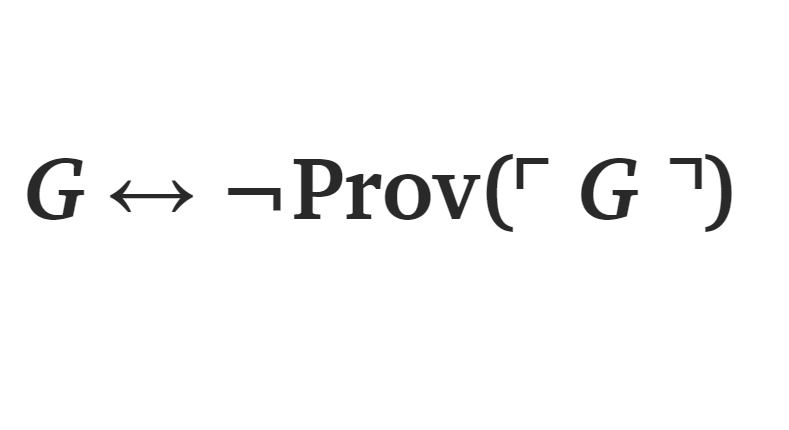
On Gödel's first incompleteness theorem.
Take the following symbolic representation of Gödel's own sentence G from the logician and philosopher Professor Alasdair Urquhart (as found in his paper ‘Metatheory’):
G ↔ ¬Prov(⌜G⌝)
The above means:
The sentence G is true if and only if it is not provable in system T.
Some readers may wondering about the second use of the symbol G and its surrounding superscripted square brackets.
This is a code number or a Gödel number.
A code number or Gödel number is a number which is used to identify something which is not a number. This means that the symbol ⌜ G⌝ is the code number of the Gödel sentence G (i.e., the symbol G without brackets). Furthermore, a Gödel number is a specific kind of code number. In mathematical logic, Gödel numbers are natural numbers which are assigned to statements (as well as to the individual symbols within those statements ) within a given system or formal language.
Now let’s get back to Hofstadter.
Hofstadter’s G Again

Hofstadter himself concluded by saying that
“knowing that G is not a theorem, we’d have to concede that G expresses a truth”.
So G isn’t — and also is — a theorem of TNT.
All this parallels (as already hinted at) the true but unproven statements in Gödelian systems. In actual fact, this is a simple rewording (or reworking) of Gödel's very own G.
To repeat.
If Hofstadter’s G were a theorem, then it couldn’t be true because it says of itself that it “is not a theorem” (of TNT). So G can only be taken as a truth if it’s also taken not to be a theorem. This, of course, exactly parallels Gödel's own G which is true in a Gödelian system — yet still unproven in that very same system.
Then Hofstadter made the (almost) obvious Gödelian conclusion when he wrote these final words:
“Here is a situation in which TNT doesn’t live up to our expectations — we have found a string which expresses a true statement, yet the string is not a theorem.”
************************************
See my related publications in Cantor’s Paradise:
(1) ‘Why Empty Logic Leads to the Liar Paradox’. (2) ‘(A) The sentence A is not true’. (3) ‘Gödel’s First Incompleteness Theorem in Simple Symbols and Simple Terms’.









No comments:
Post a Comment