“A mathematician is bound to be horrified by my mathematical comments. [] He has learned to regard them as something contemptible []."
— Wittgenstein (in his Philosophical Grammar, 1932)
Much of what Ludwig Wittgenstein (1889–1951) wrote is hard to decipher. And that’s the primary reason why there’s what can (sarcastically) be called a Wittgenstein Interpretation Industry. This also explains why many loyal Wittgensteinians get so hot under the collar when other commentators “get Wittgenstein wrong!”. Indeed, unlike many other philosophers, much of the debate around Wittgenstein’s work isn’t about whether or not what he wrote is true or false, well argued or badly argued, worthwhile or worthless, etc. — but about what he actually meant.
Lee Braver (in his Groundless Grounds: A Study of Wittgenstein and Heidegger) puts all this better when he wrote the following words:
“[Wittgenstein’s] writing style is perhaps the most obscure of all the great analytic figures, leading to an unusual state of affairs: ‘one of the most striking characteristics of the secondary literature on Wittgenstein is the overwhelming lack of agreement about what he believed and why.’ Already in 1961, the literature on the Tractatus was compared to literary scholarship in dissension and sheer mass. His opaque prose and sparse argumentation have given rise to a cottage industry of exegetical work and scholarly contention [].”
Thus all that is but a preamble to the essay which follows. It can also be said that I’m getting my excuses out of the way before I begin.
Mathematical Truth and Mathematical Correctness

“The terms ‘sense’ and ‘nonsense’, rather than the terms ‘true’ and ‘false’, bring out the relation of mathematical to nonmathematical propositions.”
— Wittgenstein (Lectures, Cambridge 1932–35)
The “late Wittgenstein” argued (at least to paraphrase or even to interpret) that if the operations on numbers result in truths, then shouldn’t it also be the case that the numbers themselves (in whichever order) have truth-conditions or references? (Perhaps the term reference is better suited here.) In basic terms, shouldn’t each number correspond or refer to something? But if the numbers themselves have no truth-conditions or references, then how can the concept of truth be carried over to the operations on numbers? Surely you can’t have one without the other.
And all that is largely why Wittgenstein emphasised what he called “correctness” (as well as mathematical “grammar”) rather than truth.
The operations on numbers also fall under Wittgenstein’s meaning is use theory.
So does the correct use of numbers also imply truth?
There may be a correct and incorrect way to operate on numbers; though is there a true way to operate on numbers? The words “truth” and “correctness” aren’t, after all, synonyms.
Wittgenstein believed that correctness is determined by rules; which are themselves a product of persons, conventions and and/or language games. Truth, on the other hand, has been deemed by many philosophers, mathematicians and laypeople to be separable from minds, conventions, etc. (i.e., as in the various philosophical realisms).
Wittgenstein himself wrote the following on rules and their role in mathematics:
“Because they all agree in what they do, we lay it down as a rule, and put it in the archives. Not until we do that have we got to mathematics. One of the main reasons for adopting this as a standard, is that it’s the natural way to do it, the natural way to go — for all these people.”
Thus, according to Wittgenstein, we can count in a correct way; though not in a true way. Truth could only enter the equation if numbers themselves were true of something else or if they referred to something else. In other words, the inscriptions or symbols must have entities to which they can correspond or refer. Only then, on a Platonist picture at least, could we talk of truth in mathematics.
Of course many people intuitively feel that there must be more to mathematics than mere inscriptions/symbols on the page and the correct rules (or correct mathematical “grammar”) for using those inscriptions/symbols. (This position is usually called formalism; though Wittgenstein went way beyond, say, David Hilbert’s formalism.) But do we think in the same way when we play a game of chess? Do we expect the pieces and the moves to somehow correspond or refer to things (whether people or events) external to the actual game of chess? It can be granted that if someone takes chess literally, then he may well think in terms of the pieces and moves corresponding — or referring - to real historical battles, political situations and well-known historical persons. (This may well be the case for certain individuals.) However, such correspondence-relations aren’t in fact needed when one plays chess. Indeed chess can be seen in purely abstract terms despite the fact that we play the game with castles, pawns, bishops, etc. More abstract forms (which have no correspondents or referents in — or to — the external world) could easily become the substitutes of castles, pawns, etc. And such substitutions would have no important impact on the nature of the game itself.
Thus — on this Wittgensteinian reading — there are correct moves in chess; though there are no such things as true moves… Of course that’s unless we’re using the word “correct” as a literal synonym for the word “true”!
[Note: Although no one expects the individual words in a natural-language statement to have their own truth conditions — the names within such statements do have their own references and other words may have their extension. Few people have demanded that connectives, prepositions, etc. have any of these things.]
Mathematical Grammar
“Consider Professor Hardy’s article (‘Mathematical Proof’) and his remark that ‘to mathematical propositions there corresponds — in some sense, however sophisticated — a reality.’ [] We think of ‘reality’ as something we can point to. It is this, that. Professor Hardy is comparing mathematical propositions to the propositions of physics. This comparison is extremely misleading.”
— Wittgenstein (Lectures on the Foundations of Mathematics)
Wittgenstein believed that mathematical statements are grammatical in nature. Thus if the grammar is in order, then the mathematics is correct. So he elaborated on the quote above with the following few words about Blaise Pascal:
“The mathematician Pascal admires the beauty of a theorem in number theory; it’s as though he were admiring a beautiful natural phenomenon. Its marvellous, he says, what wonderful properties numbers have. It’s as though he were admiring the regularities in a kind of crystal.”
So what about the following statement? -
Mathematical statements are correct because such statements are true.
That’s a possible riposte.
Wittgenstein might have simply turned that statement on its head and claimed the following:
Mathematical statements are true precisely because they’re grammatically correct.
That could be to concede that mathematical grammar is parasitical on mathematical truth. Alternatively, it might be to concede that mathematical truth is parasitical on mathematical grammar. In addition, if Wittgenstein dispensed with mathematical truth, then perhaps we can also dispense with mathematical grammar… Or at least it can be said that you can’t have one without the other.
Wittgenstein might also have accepted mathematical truth; though only when it isn’t conceived as some kind of correspondence with (or reference/relation to) abstract entities in a Platonic world.
So is it possible to make sense of mathematical truth when it’s is cashed out exclusively in terms of abiding by grammatical rules?
For a long time truth itself (regardless of mathematics) has been cashed out in many ways other than in terms of correspondence (i.e., as in the correspondence theory of truth). Thus why should mathematical truth be any different?
The question therefore is this:
Can mathematical truth be cashed out solely in terms of following grammatical rules?
What is it, then, to follow a rule?
Is it to conform to a norm and/or to a practice?
Use and Mention: “2 + 2 = 4” ≠ 2 + 2 = 4
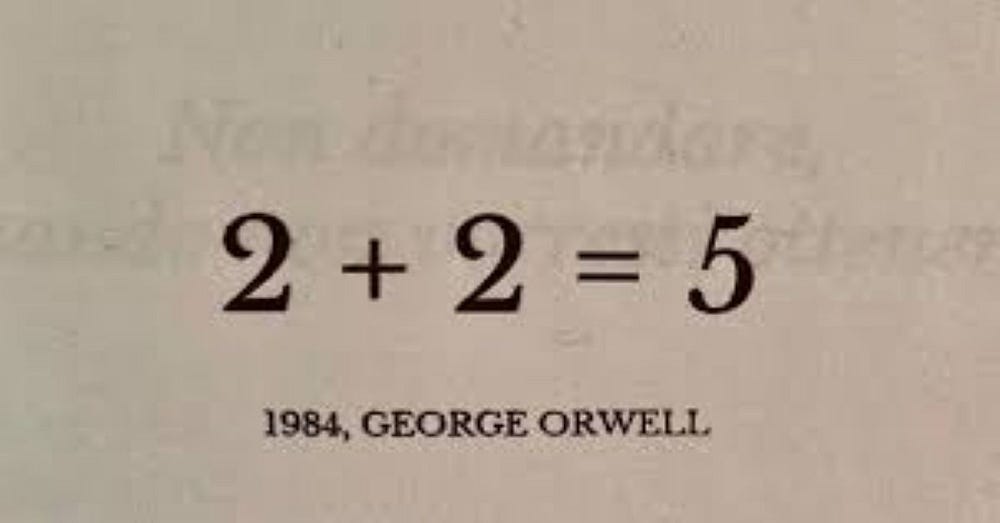
In what follows the philosophical and/or semantic distinction between use and mention needs to be highlighted. In this case, the distinction is between the linguistic expression “2 + 2 = 4” and 2 + 2 = 4. Admittedly, sometimes it’s hard to distinguish the two (I had problems in the last section) — at least in the following context and if one takes a broadly Wittgensteinian position.
In very simple terms, the distinction can be shown when it comes to the word “cat”:
Use: “This cat is very aloof.”
Mention: “The word ‘cat’ is derived from...”
The first sentence refers to the animal called a “cat”: it uses the word “cat” to refer to that animal. The second statement is about the word “cat”.
More relevantly:
Mention: “2 = 2 = 4” — a linguistic expression
Use: 2 + 2 = 4 — an (abstract) equation
(Note that the mention example above uses numbers within a linguistic expression. To be careful, some philosophers would advise using numerals or number-words like “two” and “four” instead of the symbols “2” and “4”.)
So now take this statement (a mention):
“The statement ‘2 + 2 equals 4’ is true.”
Isn’t there a rule which tells us that if we add 2 and 2, then the result will be the number 4? That said, there could be a rule which tells us this:
“The statement ‘2 + 2 equals 5’ is true and is perfectly in order.”
That is, when 2 is doubled, an additional number must be added. However, this new rule would simply be parasitical on the rule that 2 + 2 must equal 4 because it does, after all, talk of the addition of a number to the result of doubling the number 2. The rule doesn’t, on the other hand, state “2 + 2” does equal 5: it says that a number needs to be added to the sum of 4 and 4.
So let’s try a purer formulation.
Take the statement (or even rule) that “2 + 2 equals 5” without mentioning any addition of an extra number…
A Dialogue Between a Wittgensteinian and an Opponent

A Wittgensteinian:
“Why can’t 2 plus 2 equal 5? Or, at the least, why can’t I express ‘2 plus 2 equals 5’ as a rule? Indeed you’re simply assuming that the numbers I’m using have the same properties as the numbers that you’re using. Clearly, if I use my numbers in the way that you use your numbers, then evidently my statement ‘2 + 2 = 5’ will be incorrect. However, my numbers aren’t the same as your numbers. Thus in my language game (or system) 2 + 2 does indeed equal 5.”
An anti-Wittgensteinian:
“Then you’re misusing the arithmetical concepts [addition] and [equality].”
A Wittgensteinian:
“Yes, if I use the concepts [equality] and [addition] in the same way in which you use them, then evidently my statement ‘2 + 2 = 5’ will be incorrect. But my concepts [addition] and [equality] aren’t equal to yours. In my language game (or system), they work differently.”
An anti-Wittgensteinian:
“But you’ve just contradicted yourself. You said that your concepts [addition] and [equality] aren’t ‘equal’ to my concepts [addition] and [equality]. But you’ve just used the concept [equality] in the way I use it. You’ve just said that your ‘concepts aren’t equal to’ mine. And with that I agree. Therefore it would follow that the concept [equality] you use in your mathematical system isn’t equal to your use of the concept [equality] when you use it to talk about your own mathematical ‘language game’.”
A Wittgensteinian:
“Yes, you’re right. According to one language game (i.e., mathematics) I use the concept [equality] in one way. And according to another language game (talking about mathematics or metamathematics), I use the concept — or at least the word — in another way.”
An anti-Wittgensteinian:
“If that’s the case, then how the hell can we have a proper conversation if we’re using the same concepts (actually, words) in different ways? If you can arbitrarily stipulate a meaning of a concept in any way you like, then perhaps we’re not having a genuine conversation at all. We’ll simply be talking at cross-purposes.”
A Wittgensteinian:
“No, because I know that the concept [equality] is always relative to a language game. Therefore if I know what language game the concept belongs to, then I also understand the concept. I understand your use of the word ‘equality’ because I know which language games it belongs to. Therefore I can understand you and we aren’t talking at cross-purposes. All I need to determine is the language game to which the concept or word belongs. And even in my own case, I need to be aware of how I’m using a particular concept or word. I need to know which language game I’m using when conversing with other people. And you too need to be aware of which language game the people you talk to are playing — otherwise you’ll be talking at cross purposes. You may of course believe that you don’t belong to any language game or even that your position is beyond language games. However, such a position would be a meta-language game; which would simply be another language game with highfalutin ambitions.”
(*) See my ‘When Alan Turing and Ludwig Wittgenstein Discussed the Liar Paradox’.












No comments:
Post a Comment