“What is it that breathes fire into the equations and makes a universe for them to describe?”
— Stephen Hawking (from A Brief History of Time)

It is quite incredible that we don’t know what mass, spacetime, gravity, etc. are. At least if we accept Philip Goff’s account of physics. (Goff is an English philosopher.)
Don’t most laypeople believe that physics tells us about reality/Nature? Mass, spacetime, gravity, etc. are fundamental parts of reality/Nature. Yet, according to Goff, physics only tells us what these (for want of a better word) “properties” do; as well as what they’re (causally) related to.
Goff’s argument is that surely something (or some things) must be responsible for the doings. In other words, you don’t usually have a verb without an object.
So, to take just one relevant example, if mass curves spacetime, then what is it that curves spacetime? Alternatively, if spacetime (to use John Wheeler’s words) “tells objects how to move”, then what is it that’s telling objects how to move?
Despite all the above, Goff doesn’t simply stress the fact that physics only concerns itself with doings and relations. He also tells us what’s missing from this picture: intrinsic nature.
Indeed Goff goes one step beyond that when he tells us exactly what he believes intrinsic nature is. He does so in the following passage:
“What then is the intrinsic nature of matter? Panpsychism offers an answer: consciousness. Physics describes matter ‘from the outside’, that is to say, physics gives us rich information about the behaviour brought about by mass, spin, charge, etc. But there must be more to what something is than what it does; and according to panpsychism, mass, spin, charge, etc, are, in their intrinsic nature, forms of consciousness.”
Of course one can agree with Goff when he cites the problems with causal structuralism (i.e., when it comes to physics) without also accepting his position on intrinsic nature — let alone accepting his belief that intrinsic nature is actually constituted by “forms of consciousness”!
In any case, panpsychism itself will be ignored in this essay. Instead, I’ll concentrate on Goff’s take on causal structuralism in the philosophy of physics.
Gravity, Spacetime & Mass: What are They?
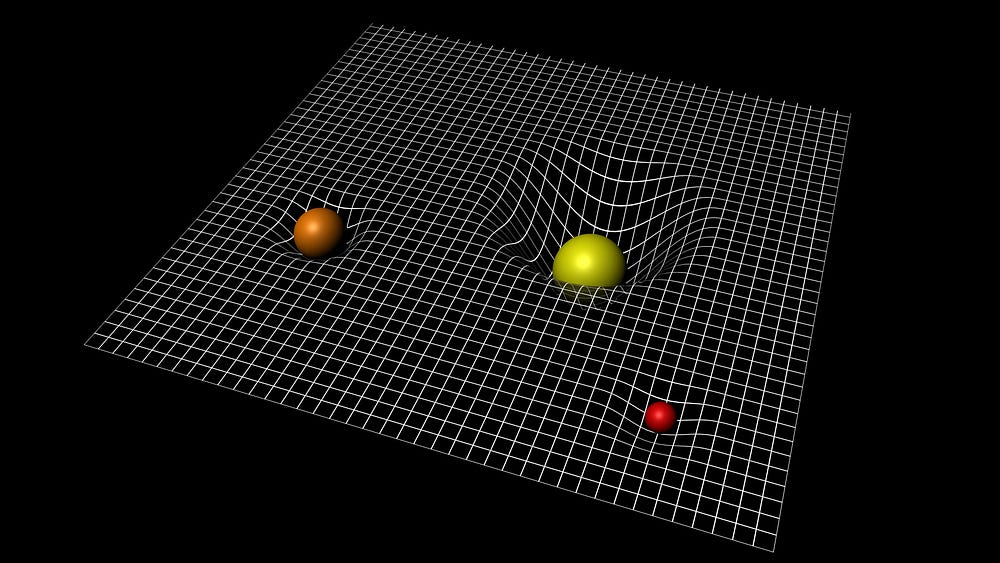
Philip Goff’s position on gravity is very useful when it comes to capturing his general position on the limitations (or simply the limitation) of physics.
Indeed Goff states something which I can only assume many laypersons will find bizarre — or, perhaps, simply puzzling. He does so when discussing Isaac Newton’s theory of gravity. Goff writes:
“Newton’s theory didn’t really explain gravity, rather it proposed a mathematical law that describes the gravitations attraction between all material entities.”
Any interpretation of the passage above will depend on what exactly Goff means by the word “explain” (as in “explain gravity”). After all, isn’t Newton’s theory a perfect explanation of gravity? Here I don’t mean perfect as in being perfectly true (or even all-encompassing). I mean perfect in the sense of giving a physicist — or even a layperson — precisely the kind of thing he or she would want. Of course, even though there is something more (e.g., Albert Einstein’s theories of relativity), then that something more still belongs to physics.
So what does Goff mean by “explain”? Alternatively, what more does he want?
Well, Goff tells us what more he wants. He also tells us what a (full) explanation of gravity should give us. Goff concludes:
“Newton didn’t explain why objects exert this force. And he admitted it: concerning the underlying mechanism that generates gravity, Newton famously said ‘Hypotheses non fingo’ or ‘I frame no hypotheses.’”
Goff’s central position is that the properties of physics are described in terms of both what they do and in terms of their relations — not in terms of what they are.
So what about space?
Take the following description of space:
“Space is one of the few fundamental quantities in physics, meaning that it cannot be defined via other quantities because nothing more fundamental is known at the present. On the other hand, it can be related to other fundamental quantities. Thus, similar to other fundamental quantities (like time and mass), space can be explored via measurement and experiment.”
This account of space (note: not Einstein’s spacetime) — at least at first sight — seems to go against Goff’s account of causal structuralism (or relational networks) in that it’s stressing the fundamentality of space. That is, it’s telling us that space “cannot be defined via other quantities”.
Bizarrely enough, this means that space’s fundamentality accounts for its relational characterisations. That is, firstly there’s the fact that space cannot be defined via other quantities. And yet then, because of that fact, space must be defined in terms of other quantities (or its relations to other parts of the/a network) precisely because of its fundamentality. (In the passage above we have the following words: “On the other hand, [space] can be related to other fundamental quantities.”)
This means that it’s not simply that space has no qualities beyond its relations or doings. It’s also a case of space being so fundamental that there’s no choice but to characterise it relationally or in terms of its doings.
Goff also seems to be — at least partly — correct when it comes to mass.
In most — or even all — accounts of mass, we aren’t told what mass is. Take this definition:
“Mass is both a property of a physical body and a measure of its resistance to acceleration (rate of change of velocity with respect to time) when a net force is applied. An object’s mass also determines the strength of its gravitational attraction to other bodies.”
In the passage above we’re told that mass is a “property of a physical body”. This means that we aren’t only being told what mass does — as Goff himself usually argues. It’s being said above that mass (as it were) belongs to physical bodies: it’s a property of physical bodies.
Similarly, when it’s stated that mass is a
“measure of its resistance to acceleration (rate of change of velocity with respect to time) when a net force is applied”
we’re not being told what mass is. Mass — at least in this instance - is what accounts for resistance in physical bodies. (Specifically, it’s what’s responsible for the resistance to acceleration.) In that sense, it’s like the everyday notion of weight in that weight isn’t a thing — it is what things (as it were) have. And things have mass too.
In the same sense, when we’re told that
“mass also determines the strength of its gravitational attraction to other bodies”
we’re not told what mass is here either. We’re only told what effect the mass of a body has on other bodies. This means that the mass of one body does things to other bodies.
Yet what is this mass which does things to other bodies?
Chess Pieces & Particles: What are They?

In order to stress his position on intrinsic nature, Philip Goff gives the example of chess pieces. (See ‘The Intrinsic Nature Argument’.) He writes:
“Consider the following analogy. Imagine you have a chess piece on a board. You may know what the the chess piece does, how it behaves, if it’s a bishop, let’s say, it moves diagonally. But there must be more to the nature of the chess piece than what it does. There must be some way the chess piece is in and of itself, independent of its behaviour. It may, for example, be made of wood or plastic. When we ask how the chess piece is in and of itself, we are asking about its intrinsic nature.”
Surely this is a poor “analogy” — and it is so in many ways.
Philip Goff would have been wiser to choose (as an example) human beings, trees or even samples of water to best emphasise the distinction that can be made between what human beings/trees/samples of water are and the relations they take part in — or the things they do. After all, for centuries philosophers galore have made the distinction between the intrinsic (or essential) properties of human beings/trees/samples of water and their extrinsic (or contingent) properties. (Note the distinction between “intrinsic” and “essential” and “extrinsic” and “contingent” in the final section - a distinction which doesn’t really matter at this juncture.)
None of the above works for the game of chess or for individual chess pieces.
For a start, aren’t chess pieces entirely defined by what they do — or what they can do? This isn’t usually seen to be the case when it comes to human beings, trees or samples of water. (That said, some philosophers do argue for this relationist position even when it’s applied to human beings — or, perhaps more accurately, to persons.)
In any case, it doesn’t matter at all what chess pieces are made out of — whether that’s Goff’s own “wood or plastic” or anything else. Indeed chess pieces don’t need to be made out of anything. For example, chess can be played on a computer. Unless, in this case, chess pieces are “made of” the physical hardware (e.g., the zinc, silicon, aluminium, etc. which make up the circuits, transistors, etc., and even the electrical currents) which subserves the chess-piece icons which we see on a screen… But surely that’s pushing things a little.
Chess is essentially an abstract game. Cups or persons aren’t abstractions — although they can be specified functionally. And even a particular wooden or plastic chess piece isn’t an abstraction. But chess as a game, and what each chess piece represents, are abstractions.
Goff goes on to compare chess pieces to subatomic particles. He concludes with the following words:
“Similarly for the electron, independently of what it does in relation to other particles, there must be some way the electron is in and of itself. And yet physics leaves us completely in the dark about the intrinsic nature of the electron.”

So it’s ironic, and doubly helpful, that the theoretical physicist Paul Dirac (1902–1984) once compared particles to chess pieces too. He wrote (as quoted in the biography The Strangest Man: The Hidden Life of Paul Dirac, Quantum Genius) the following words:
“In chess, we have various chessmen, kings, knights, pawns and so on. If you ask what chessman is, the answer would be that it is a piece of wood, or a piece of ivory, or perhaps just a sign written on paper, or anything whatever. It does not matter. Each chessman has a characteristic way of moving and this is all that matters about it. The whole game of chess follows from this way of moving the various chessmen.”
The obvious point must again be made here.
Chess is defined (or characterised) by how the chess pieces (to use Dirac’s own term) “behave” or “move”. Nonetheless, we can go along with Goff and at least accept that chess pieces must still physically exist… Well, no, and as already stated — not if chess is played on a computer. In other words, nothing hangs on what a chess piece is made of — even if a chess piece is always made of… something. Thus if we characterise a plastic bishop, and mention its synthetic makeup, its feel, colour, etc., then we aren’t characterising this chess piece qua its role as a bishop. We’re actually characterising what the bishop piece is made out of. And what it’s made out of is completely irrelevant to it being a bishop in the game of chess.
So, in a strong sense, a chess game as a whole — or the pieces taken separately — can be entirely explained in mathematical and geometrical terms… with little or no (as it were) physical remainder.
But what of particles?
The analogy between chess pieces and particles may break down anyway.
It’s of course the case that the way chess pieces move or behave isn’t dependent on their being made of wood, ivory, or anything else. Yet when it comes to particles, surely it can be argued that their physical nature may — or even must — determine how they behave or move. After all, when taken together, particles don’t constitute an abstract game (or an abstract anything), and every single particle isn’t an abstraction either… Unless one is a Pythagorean when it comes to physics!
Yet, to put it bluntly, Paul Dirac’s own position seems to be eliminativist when it comes to particles. It is so because particles’ movements (or doings) take the place of… things. Yet if Dirac’s position is eliminativist, then why did he speak of “particles” at all? Unless, of course, Dirac simply took the word “particle” (or even “electron”) to be shorthand for specific types of behaviour or movement. (Much of this seems to parallel — at least to some extent — the relations-no-relata stance of ontic structural realism.)
Despite all that, this simply raises the same question again:
What is it that behaves (or moves) in such specific ways?
Surely you can’t have behaviour (or movement) without things (or particles) which carry out that behaviour (or which move).
Philip Goff on Causal Structuralism

Philip Goff takes up a position against what he calls causal structuralism. To be more accurate, Goff doesn’t exactly reject causal structuralism. It’s more a case that Goff believes that it leaves something out — just as he believes that physics itself leaves something out!
The following is Goff’s take on the causal structuralist position on mass:
“What is mass? For a causal structuralist, we know what mass is when we know what it does, i.e., when we know the way in which it curves spacetime. But to really understand what this really amounts to, as opposed to merely being able to make accurate predictions, we need to know what spacetime curvature is. What is spacetime curvature? For a causal structuralist, we understand what spacetime curvature is only when we know what it does, which involves understanding how it affects objects with mass. But we understand this only when we know what mass is. We find ourselves in a classic catch-22: we can understand the nature of mass only when we know what spacetime curvature is, but we can understand the nature of spacetime curvature only when we know what mass is.”
To state the obvious.
If we’re (only) doing physics, then — almost by definition — any account of mass is going to bring in spacetime (among other things from the lexicon of physics); and any account of spacetime is going to bring in mass…
So it’s hard to know what other option a physicist would have.
Yet, of course, Philip Goff is asking philosophical questions. And that must mean that the physicist — almost by definition — won’t be able to answer his philosophical questions (at least not qua physicist).
Think about this.
Goff is demanding an “account” of mass that doesn’t mention spacetime, gravity, or any other property specified by physics. Similarly, Goff is demanding an account of spacetime that doesn’t mention mass, gravity, or any other property specified by physics.
In other words, Goff is demanding that physics stop being physics.
Now to be fair to Goff (or to backtrack a little): he may not be expecting physics to stop being physics. Instead, he may simply be making the point that physics alone can’t (as it were) join the dots. That is, physics is good at what it does. However, it doesn’t provide us with a complete picture as to what reality is. Philosophy, then, must do that job. (One would hope that Goff also believes that philosophy must do that job on the solid grounding which physics has already provided.)
Goff himself says as much in a few places.
For example, straight after the just-quoted words above, Goff writes:
“I agree that mass can be uniquely identified — as it were, homed in on — in terms of its place in the abstract pattern of causal relationships realized by the entire network of physical properties.”
In other words, Goff fully accepts that mass and spacetime are “uniquely identified” in terms of an “abstract pattern of causal relationships realized by the entire network of physical properties”.
Yet all that alone doesn’t provide us with a complete picture of reality.
And elsewhere Goff — alluding to a well-known passage from Stephen Hawking (which opened this essay) — writes:
“The equations of physics allow us to predict the behaviour of matter with great precision. But is is the intrinsic nature of matter that breathes fire into those equations. And on this topic physics has nothing to say.”
Again, physics is great… though only within (its own) limits. (It can also be said that some/many physicists have happily accepted such limits.) In this case, physics is great for “predict[ing] the behaviour of matter” and it does so “with great precision”. The problem is — or so Goff believes — that it leaves out what he calls intrinsic nature — and it’s intrinsic nature which “breathes fire into the equations”!
Goff is simply assuming that there is such a… thing… as intrinsic nature. Not only that: the term “intrinsic nature” is purely an invention of philosophers. That is, very few physicists will have even heard of the term. Of course, that fact alone isn’t a good reason to dismiss either the usage of the term “intrinsic nature” or even the existence(?) of intrinsic nature. And that’s primarily because Goff and many other philosophers have provided arguments as to why there must be “intrinsic properties” and therefore intrinsic nature.
So it may well be the case that physics doesn’t provide a complete picture of reality or Nature.
The Circularity Objection
Philip Goff happily admits that some of the philosophers who have a problem with causal structuralism offer at least one often-used and poor argument against it. This poor argument Goff calls “the circularity objection”. Goff hints at that objection in the following passage:
“Causal structuralism, they say, implies a kind of holism, whereby the nature of a given thing cannot be understood in isolation from all other things. And so the very demand for an account of ‘mass’ in isolation from ‘spacetime curvature’ would seem to be premised on the assumption that causal structuralism is false. If causal structuralism is true, then mass and spacetime curvature (and everything else) must be defined ‘all at once.’”
More specifically, Goff tackles the circularity objection in the following way:
“Causal structuralists often content that the circularity objection begs the question [] by assuming that the definition of a given property, such as mass, must be given in isolation from all other properties.”
This counter-argument against causal structuralism seems highly abstract in that it’s hard to even comprehend what a
“definition of a given property [] in isolation from all other properties”
would even be like. Surely such a definition is bound to bring in at least some other properties… or some other things. Perhaps not properties from inside the (as it’s often put) “holistic network” to which the given property is supposed to belong… but at least some other properties. In other words, the whole notion of isolation seems suspect.
And it doesn’t help here that we’re talking about “properties”. That’s because it’s not clear how that word is meant to be read (or interpreted). That said, it does seem to lead to David Lewis’s position on what he called “intrinsic properties”; which may well be Goff’s main source in his position on what is intrinsic. (See final section on David Lewis’s position.)
Take the case of mass.
Even if mass can be defined (or characterised) in terms that don’t include what it does or the other physical properties it’s related to, that characterisation would no doubt still include things outside mass itself.
Again, it’s hard to even imagine how this could be any other way.
As stated, how can the “nature of a given thing” ever be “understood in isolation from all other things”? Or, perhaps less strongly, how can the nature of a given thing ever be understood without bringing on board at least some other things? (Even if not Goff’s “everything else”.)
What would such an (as it were) atomic understanding (or account) of mass — or anything else — even look like? What’s more, this question makes even more sense if we think of classical examples such as cups, trees, and people — how could we give an account of a cup, tree, or person in isolation from all other things? More relevantly, it’s difficult to even comprehend giving an account of mass, spacetime, or gravity in isolation from all other things. What would such an account look like?
Yet there are problems with holism too.
Can we have holistic networks without things? Or, at the very least, can we have causation without conditions, states, etc. which do the causing? Surely we can’t only have structures or networks.
These questions are often asked about all kinds of structuralism. As it is, I won’t tackle this thing/network (structure) “binary opposition” here because it’s already been tackled in great detail many times before. (Indeed I’ve written on this subject myself.)
So holism may be an important notion (in this and in other cases); although surely it can’t be the whole story.
For example, in order to be part of a holistic network, each part of that given network must have some defining features (or individuating conditions) which separate it from the network itself — otherwise, how could it be a part of it… or a part of anything? What would make it apart? How is any part of a network distinguished from the network itself in the first place?
Goff also seems to play a sleight of hand here. He jumps from emphasising networks to then saying that
“mass and spacetime curvature (and everything else) must be defined ‘all at once’”.
Why must literally “everything else” be defined in these cases? Why not only a given network and its parts? In addition, what do the words “defined all at once” even mean? That is, how can anything — let alone everything — be defined all at once? I doubt that a causal structuralist would claim they could define anything — let alone everything — all at once or even be implicitly committed to the idea.
David Lewis on Intrinsic Nature?

This final section is a rather technical (philosophical) discussion of David Lewis’s ontological position on what he called “intrinsic properties”. Some readers — especially those who’re primarily interested in physics — may find it a little arcane and irrelevant.
In any case, it may be the case that Philip Goff’s position on intrinsic nature is inspired by the work of the American philosopher David Lewis (1941–2001). So why is that? Well, take Lewis’s definition of “intrinsic properties”:
“A thing has its intrinsic properties in virtue of the way that thing itself, and nothing else, is.”
Lewis’s wording above is almost identical to some of the passages from Goff that have been quoted earlier in this essay.
So could there ever be such a state as “the way that a thing itself is” regardless of everything else? That is, regardless of its relations to other properties/objects/events, its place in time and space, and so on?
This position is taken to its most extreme (or perhaps ridiculous) in the following statement:
Object a would still have intrinsic property P if after the entire world around it disappeared, a would still have P.
Perhaps there’s a midway position in that it can be argued that there are indeed intrinsic properties; though they still have vital (or even essential) relations to extrinsic properties. That is, extrinsic proprieties may determine — to some extent at least — intrinsic properties. That said, it may be countered that because objects are such-and-such-a-way, then they can only be affected or determined in particular ways precisely because they have the intrinsic properties which they do have. That may mean that there may be some kind of mutual relation between intrinsic and extrinsic properties. Indeed, as stated, there may be no “way” an object is regardless of its relations to other things — or to extrinsic properties.
In addition, at first sight Philip Goff’s philosophical term “intrinsic” (as in his “intrinsic nature”) appears to almost be a synonym of the philosophical term “essential” (as in “essential nature”). Indeed it’s tempting to use the latter — rather than the former — word.
There are differences, however.
As often happens in philosophy, there are indeed (slight) differences between the two terms which seem to have the same — or just similar — content. Or, at the very least, there are different definitions of the terms “intrinsic property” and “essential property”. Nonetheless, it can still be said that the two categories are very closely related. Or, to put that another way, this (to use Derrida’s term) “sign substitution” of the word “intrinsic” for the word “essential” would never have occurred if both essentialism and anti-essentialism had never been such important parts of the Western philosophical tradition.
Yet, as hinted at, Goff’s position on intrinsic nature still isn’t identical to most traditional forms of essentialism.
In most forms of essentialism, things can have essential properties which aren’t replicated in (or by) the essential properties of other things. Thus such essential properties can be specified in all their particularity (even in the case of the — Aristotelian - essence of say, a particular species or kind). Goff’s intrinsic nature, on the other hand, must be instantiated in all sorts of different things — from mass, spacetime, and particles to neurons and even rocks. In other words, that intrinsic nature is the same in (almost) all things. Indeed, in Goff’s own broader ontology, that intrinsic nature is experiential or phenomenal in nature!
In addition, in traditional philosophy, whenever one has essential properties, one must also have contingent properties. Yet this would mean that on Goff’s account of mass, spacetime, particles, and the other properties of physics, what they do (along with their relations) would be deemed to be contingent. And — in physics at least — that seems crazy. If anything, what the properties of physics do is better seen as being essential to what they are. That said, a philosopher can choose the option of rejecting this essential/contingent binary opposition altogether — especially when it comes to mass, spacetime, particles, and other things in physics.
To sum up.
Some metaphysicians highlight the difference which can be made between the following:
(1) Properties which objects have independently of any external factors acting upon them (i.e., intrinsic properties).
(2) Properties which are deemed to be the way they are regardless of what’s external to them (i.e., essential properties).
So, if this logic is applied to Goff’s own examples, then the intrinsic natures of mass, spacetime, gravity, particles, etc. would be what they are independent of any external factors acting upon them. Similarly, such natures will be what they are regardless of what’s external to them.
Yet surely all these arcane distinctions and subtleties (in ontology) seem crazy when applied to the fundamental properties of physics.











No comments:
Post a Comment