Donald Hoffman is attempting to “come up with a mathematically precise theory of consciousness and [] space, time, and matter”. That project involves an essential commitment to idealism. But how substantive is the maths in his project?

[The title above is an ironic take on Donald Hoffman’s ‘Reality is Eye Candy’, which was a presentation he gave in 2017 at a SAND conference.)
Professor Donald Hoffman often uses phrases such as “precise mathematics” and “mathematical models” in reference to his own philosophical position — conscious realism. Hoffman explains why he does so in the following words:
“Part of my background is in psychophysics. This is the science of studying conscious experiences and building mathematical models. Your conscious experiences are not random things. We do careful experiments and can write down mathematical equations that actually describe the conscious experiences you will have. They’re mathematical, so conscious experiences can be described by mathematics.”
As just stated, Hoffman often mentions “mathematical models”. However, he rarely says what he means by those two words. And he rarely offers us any examples of these models. (The ones I’ve found will be discussed later.)
There may be a good reason as to why Hoffman doesn’t give us any examples. For example, he says that we must
“admit that maybe consciousness can be described with mathematics”.
Hoffman doesn’t say that consciousness has been “described with mathematics” here: he uses the word “maybe” instead. Yet elsewhere Hoffman keeps on talking about his mathematical models of consciousness (as well as of experiences).
Models of “conscious experiences”?
What form do they take?
And what does it mean to claim that scientists like Hoffman
“can write down mathematical equations that actually describe the conscious experiences you will have”.
Does Hoffman may mean that there are mathematical models of the physical bases or correlations of what he calls “conscious experiences” or consciousness itself?(See ‘Neural correlates of consciousness’.) That is, is Hoffman simply taking about what goes on in third-person (physical) brains — along with observable physical and verbal behaviour — when such things are studied by scientists?
If so, then any commitment to correlations, brains and behaviour would make Hoffman’s position very much like that of those neuroscientists, psychophysicists and other scientists who’re also physicalists…
Yet Hoffman is strongly against physicalism.
More relevantly, Hoffman is an idealist who’s stated that “brains and neurons do not exist unperceived”.
That, at least in itself, isn’t a contradictory position on Hoffman’s part. It simply means that Hoffman’s position on what (in this case) brains and neurons actually are needs to be made explicit — at least to all those people who aren’t aware that he’s an out-and-out idealist.
But what about having mathematical models of conscious experiences themselves?
Of course many scientists of mind and consciousness reject this “binary opposition” in that they don’t even attempt to divorce consciousness and mind from the brain. And the primary reason why they don’t do so is that most of them are either explicitly or implicitly committed to physicalism. Indeed Hoffman himself is keen to stress the fact that most scientists (specifically when it comes to the brain, mind and conscious) are — if often tacit — physicalists (see here).
So, again, how does Hoffman fit into this debate?
The general point here, then, is that mathematical models exist in physics, biology, economics, etc. Yet can there also be mathematical models of experiences and conscious agents?
In terms of the latter, the answer is yes… in a sense. That is, only if the verbal and behavioural actions of “conscious agents”, along with what happens in their physical brains, are being modelled…
Yet all that isn’t only what Hoffman is attempting to do.
Conscious Realism
Donald Hoffman often uses the word “we” when he should really use the word “I”. Take this eulogy to his own conscious realism. Hoffman writes:
“Here there is good news. We have substantial progress on the mind-body problem under conscious realism, and there are real scientific theories.”
It can be conceded that Hoffman has a few postgraduate workers, and even a few fellow professors, working with him on his conscious realism. However, phrases such as “we have substantial progress on the mind-body problem” seem a bit too grand. However, it’s the passage which follows which is relevant to this essay. Hoffman continues:
“We now have mathematically precise theories about how one type of conscious agent, namely human observers, might construct the visual shapes, colors, textures, and motions of objects [].”
Now that’s fair enough.
It can easily be seen how scientists (cognitive scientists) can construct “mathematically precise theories” about how “human observers might construct the visual shapes, colors, textures, and motions of objects”. The thing is that Hoffman goes much further than this. He has done so by entering the domain of speculative philosophy. Not only that: the reference to constructing shapes, colours, and the motions of objects can all be placed under what’s often been called “third-person science”. That is, in such a science, the researchers will rely primarily on two things:
1) The “reports” of the subjects in scientific experiments.
2) The neuroscience, etc. of vision, etc.
Hoffman moves beyond all that. He claims to have constructed a “mathematically precise” theory (or “model”) of consciousness, experiences, cognitive agents, etc. too. In addition, Hoffman also uses such mathematical models to defend (or simply describe) his philosophical position of conscious realism. Now what we have here is a huge jump from the neuroscience/cognitive science (mentioned in the quote above) to Hoffman’s speculative philosophical position.
Why the Maths?
The question is simple. When Hoffman says that his theory
“gives mathematically precise theories about how certain conscious agents construct their physical worlds”
what does he mean?
More precisely, in what way are numbers and other mathematical tools used to explain how “conscious agents construct their physical worlds”?
This can easily be answered in one way.
Numbers or mathematics generally can be used to describe or explain just about anything.
For example, if I randomly throw a deck of cards on the floor, the positions of all the individual cards can be given a precise mathematical description…
But why bother?
The other question is about how exactly maths makes sense of what goes on in minds or consciousnesses. Here again maths can be used (perhaps arbitrarily or pointlessly) to do so. More to the point, what work is the maths doing in Hoffman’s philosophical position of conscious realism?
Hoffman himself compares what he’s doing to what Alan Turing did. In Hoffman’s own words:
“[T]he tip from Turing is that Alan Turing decided to give a theory of what is computation and he came up with this really simple formalism. A little machine that has a finite set of states finite set of symbols some simple transition rules and it turned out he could prove that any computation could be done by this simple little device called the Turing machine and that was what launched the theory of computation computer science [].”
Consequently, Hoffman continues by asking us this question: “[C]an we do the same thing for consciousness?” That is:
“Can we come up with a simple formalism which will handle all aspects of consciousness?”
And, again, in the following we may have a category mistake when Hoffman asks this question:
“Can we come up with a mathematically precise theory of consciousness and, from that, boot up space, time, and matter?”
What’s more, Hoffman tells us that he “think[s] [that] a precise mathematical science of consciousness is possible”.
Models as Idealisations
No one will have a problem with the fact that mathematical models can — or always do — idealise what it is they’re modelling.
For example, this is the case with ideal gases, point particles, massless ropes, and lots of stuff in boxes (see Lee Smolin’s “physics in a box”). However, it’s often the case that these “idealisations” (or simplifications) go way too far.
So is this true of Hoffman’s models of consciousness, conscious agents and the rest?
Here it also needs to be stressed that real situations (or things) in the world are very complicated and thus models — especially Hoffman’s models — may be extremely approximate in nature. However, perhaps the problem is not even approximation when it comes to Hoffman’s supposed “modelling” of consciousness, experiences, “conscious agents”, etc.
Yet idealisations and simplifications are often very-good things.
For a start, a model must provide us with more than “empirical data”. Put simply, models serve a purpose that’s beyond any painstaking description of every aspect of what it that’s being modelled. And it’s precisely because models — all models (by definition) — go beyond that data that there can be the following problems:
1) Models can oversimplify.
2) Models can bear little relation to what it is they model.
3) The relations between a model and what it models can be very vague, weak and even purely metaphorical/analogical — and that can even be the case when the model utilises much mathematics.
All this means that each mathematical model also has to take into account the to and thro between accuracy and simplicity. These and other scientific criteria are always being played against each other. This also means that other factors must come in — such as the “predictive power” of the model. In addition, simplicity is supposed be cherished in the theories of physics and when it comes to mathematical modelling. Thus, if a model is complex, then it will more faithfully reflect the thing that is modelled. If it’s too complex, on the other hand, then it won’t serve the purpose of being a model very well. (The complex model may be hard to analyse and difficult to understand.)
Now how much of all the above also applies to Hoffman’s models and what he claims about them?
This means that Hoffman’s mathematical models (if they are mathematical models) need to account for the question as to whether or not they really do describe systems (or any given phenomena) accurately. In that sense, Hoffman’s models face the same problem which he stresses human “perceptions” face in his (part) evolutionary account of conscious realism.
**************************
Part Two
Examples of Hoffman’s Models
The following are a few examples of Hoffman’s “mathematical models” — or mathematical charts (i.e., they’re hardly even mathematical graphs).
Firstly, we have this mathematical model of what Hoffman calls a “conscious agent”:
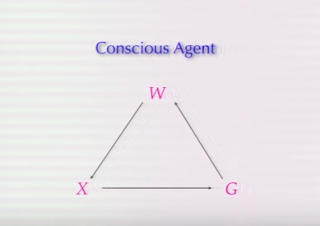
Hoffman uses the (supposedly) mathematical symbols of W, X and G in the above:
W = “a world”
X = an “experience”
G = a “conscious agent’s action”
Now once you have these symbols, you can play with them. In Hoffman’s own words:
“We can translate this into some mathematical symbols. We have a world W, experience X and action G.. and then we have a map [see next image], a Markovian kernel… and an integer counter [n] which is going to account for the number of perceptions you have [].”
And so on. And where you have mathematical symbols, you often also have maps, graphs, grids and suchlike. Hoffman makes use of them too.
So what we have is a triadic set of relations between W, X and G.
Does it tell us anything? Is it gratuitous? And even if it’s not actually mathematical in nature, does it still help us in some way?
For one, as mentioned earlier, this model is certainly an idealisation (or a simplification): all we have represented is a world (W), an experience (X) and an action of a conscious agent (G).
So why only these three (as it were) variables?
Why a single experience and a single action? (Unless X is meant to be a symbol for experiences or experience in general.) And why are X and G seemingly taken in separation of the rest of W? What’s more, how would an externalist or anti-individualist take this almost Cartesian position on a world, an experience and an action? And what about the agent (G) and his/her/its embeddedness in the world (see ‘Embodied embedded cognition’)?
It’s of course the case that Hoffman’s conscious realism may provide all the answers to these questions
So to recap.
Hoffman’s graph above is seemingly scientific. We have the symbols W, X and G for a start. Not only that: the letters are connected in a geometric graph…
But so what?
How does this graphic and symbolic representation help matters? More importantly, what does it really say? And is this really a mathematical model?
And then Hoffman goes deeper — or at least his next graph is more complex than the first one.
Now we have this:
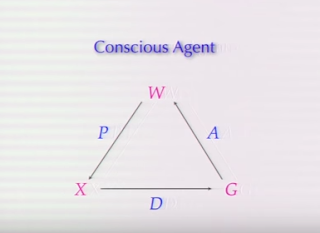
Here we have extra “mathematical symbols” and thus more (supposedly) scientific rigour.
In addition to the symbols W, X and G, we now also have the symbols P, A and D. Thus:
A = “action map”
P = “a Markovian kernel”
D = “a perception map” or a “decision map”
N = “an integer counter” which “counts the number of perception which you have”.
According to Hoffman, “a conscious agent is just [yes, just] a sextuple” — that is, “(X, G, P, D, A, N)”.
This means that the connecting line from W (a world) to X (an experience) is symbolised by P (Hoffman’s “markovian kernel” — see ‘Markov kernel’). And X’s connecting line to G is symbolised by D (a “perception map” or a “decision map”). That is, an agent carries out an “action” in a (or the) world.
Again, how does that model help?
And is the model accurate?
What sort of world (if a conscious agent’s world ) can be summed up by a “sextuple” (X, G, P, D, A, N) — even if we acknowledge the importance of idealisation or simplification?
Things get even deeper here:

Here we have a symbolic and graphic representation of “two conscious agents”, not one. In addition, we have N₁ and N₂ (both “integer counters”).
What does the image above really tell us?
If we didn’t get much meat out of the left-hand side of this image (as quoted above), then how can we get much more meat when we have both sides taken together?
Finally, we have this:
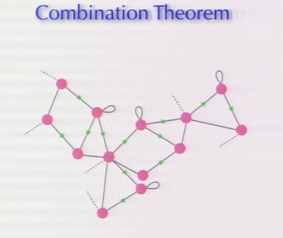
In the above, “each dot is a conscious agent” and “each link is a connection between conscious agents where they are communicating with each other”.
Even Hoffman must admit that the placings of the agents (the pink dots) and the resultant shapes of these agential interrelations are completely arbitrary. (There are symbolisations of triadic interrelations and quadratic relations; which, in turn, are related to other geometric relations.) This, however, may not matter to the philosophical point that Hoffman is attempting to get across.
Three things are now worth mentioning here:
(1) Why the use of the mathematically-sounding title “combination theorem” (see mathematical combination)?
(2) Why is the above a theorem? (More mundanely, why use the word “theorem” at all?)
(3): What does Hoffman’s graph actually give us?
Conclusion
To offer a sceptical conclusion.
Perhaps all that Hoffman means by his frequent references to “using precise mathematics” (or, more often, to using “mathematical models”) is simply the use of what he calls “mathematical symbols”; which, in turn, are then placed in graphs (such as in those above).
Yet mathematical symbols can be used for anything and they can be used by anyone.
This raises the following question:
What does Hoffman mean by the words “mathematical symbol”?
Is Hoffman really doing something that’s very different to what Julia Kristeva did in the following passage? -

And what about this “equation” from Jacques Lacan? -
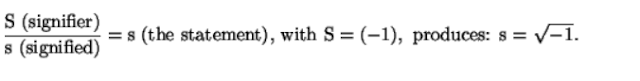
It’s not being said that Hoffman’s models are entirely in the same ballpark as the other two outré examples. However, they’re still largely gratuitous. More importantly and finally, it can be argued that Hoffman’s mathematical symbols are used to simply (as it were) tart up his speculative philosophical positions...
****************************
*) See my ‘A Contradiction in Donald Hoffman’s (Idealist) Fitness-Beats-Truth Theorem’, ‘Donald Hoffman’s Long Jump From Evolutionary Biology/Theory to Highly-Speculative Philosophy’ and ‘Donald Hoffman’s Case For An Idealist and Spiritual Reality’.









No comments:
Post a Comment