Kitty Gail Ferguson was born in 1941. She’s a very successful and excellent American science writer who’s written books on Stephen Hawking, Tycho Brahe, Johannes Kepler and Pythagoras.
Why These Constants of Nature?

Kitty Ferguson asks various questions about the constants of nature (as found in her brilliant book The Fire in the Equations). She asks us why the “fundamental forces” are the way they are. (This question also ties in with other questions about their necessary or contingent nature.) Namely:
“[N]o scientific theory we have at present can tell us why the speed of light and the strengths of the fundamental forces of nature are what they are.”
So let’s reformulate that passage as a simple question:
Why is the speed of light, the strengths of the fundamental forces of nature, etc. the way that they are?
Can we say that these values and strengths just are the values and strengths that they are? They have to be of some value and strength. The fact that they have the values and strengths that they have is entirely contingent. However, if the values and strengths were necessary, then perhaps there would be answers to Kitty Ferguson’s questions. And, of course, all her questions are tangentially — as well as tacitly — linked to the anthropic principle; and, in some cases, the existence of God.
Take this more specific question:
Why is the speed of light 186,000 miles per second?
The speed of light is 186,000 miles per second because if it were slightly less (it can’t be more), then it wouldn’t be light. It would be something else. That is, if the speed of light were something else, then it wouldn’t be light that’s being discussed.
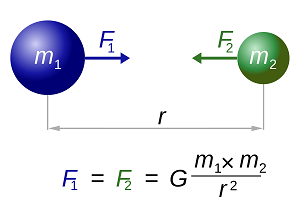
Now take this question:
Why does gravity have the strength and value that it has on earth and elsewhere?
Gravity has the force and value that it has because it wouldn’t be gravity if it had a different strength and value. It would be something else. The same goes for this question:
Why is the charge of an electron -1.6 x 10–19 coulomb and its mass 9.11 x 10–31 kilograms ?
The mass and charge of all electrons is x and y because if they weren’t that mass and charge, then they wouldn’t be electrons. They would be something else.
Nonetheless, all this seems to be truer of all electrons than of gravity and the speed of light. That is, it seems easier to conceive of a different speed of light, or gravity with a different strength and value, than it is to accept electrons with different masses and charges.
Why These Symmetries?
Ferguson says the same kind of thing about symmetries in the universe. She writes:
“[W]e might ask whether there are underlying reasons why this symmetry and not another should be the one to apply in our universe.”
We can also rephrase the passage as a simple question:
What are the underlying reasons why this symmetry and not another one should be the one which applies in our universe?
Again, there had to be some kind of symmetry — that is, if there’s any kind of symmetry at all. Sure, other kinds of symmetry might have been instantiated. They weren’t. (Again on the anthropic view, we can say that this question couldn’t have been asked without the given symmetries.) Thus perhaps the question is whether or not there was something before our symmetries; something responsible for our symmetries; or something more basic than our symmetries.
Why This Mathematics and That Logic?

Finally, Ferguson asks similar questions about mathematical logic. Thus:
“It’s a question of profound importance whether mathematical consistency required an Inventor. I’ve heard it asked at the end of public lectures on physics: ‘Is mathematical consistency as we know it the only way it COULD be — or is it conceivable it could be something different?…’ If the lecturer is a scientist or mathematician, he or she may answer that mathematical consistency just is.”
This too can be put as a simple question (though this time using Ferguson’s own words). This is her question:
“Is mathematical consistency as we know it the only way it COULD be — or is it conceivable it could be something different?”
The idea that mathematical consistency would need an inventor may strike some (or even many) people as ridiculous. Nonetheless, it may still be a good (or legitimate) question.
As for the possibility of alternative mathematics.
Some say that even the question can’t be constructed without begging the question. (This, of course, doesn’t rule out complementary or even rival mathematical systems, incompleteness, inconsistency, etc.)
As for logic.
If we must start with the basic building blocks of logic (first forcefully stated as long ago as Aristotle), then the very idea of truly independent logics is rejected by some (or many) logicians and philosophers — even by by some of those who accept paraconsistent and dialethic logics. Or as the philosopher Dale Jacquette once put it:
“Even paraconsistent logics that tolerate logical inconsistencies without inferential explosion, that accommodate contradictions but do not authorize the logically valid deduction of any and every proposition, do so according to strict rules, as strict as the rules that govern Aristotle’s syllogisms.”
Now the passage above isn’t saying that the “strict laws” of paraconsistent logic are the same as Aristotle’s. However, it is saying that there are rules in paraconsistent logic which — seemingly — aren’t even called into question. They are simply accepted.
So now perhaps we can say that same about the constants of nature; the symmetries which exist in our universe; and the basic “rules” of logic and mathematics.










No comments:
Post a Comment