Why Empty Logic Leads to the Liar Paradox

i) Introduction

ii) Empty Syntax

iii) Roger Penrose on Mathematical Formalism

iv) The Logical Syntax of Sentences and Premises

v) The Liar Sentence

vi) Conclusion

Many philosophers and logicians have analysed the forms of arguments and shown us that the same forms occur across many different cases. They’ve also shown us that when it comes to what are called argument-forms, the semantic content of the premises doesn’t (really) matter as long as the argument-form (which involves the proper use of the symbols for the premises and logical operations) is adhered to. 

This piece also deals with the form (or syntax) of the premises (or sentences) themselves. It attempts to show the philosophical consequences of premises (or sentences) being taken to be without semantic content. This is to deal with something more than the simple fact that the semantic content of premises (or sentences) can be ignored by (formal) logicians: it’s an argument that in some cases (such as the sentence “This sentence is false”) the premise (or sentence) doesn’t have semantic content in the first place (i.e., even after that content is analysed or determined). More specifically, an attempt is made to show that if a sentence in an argument has no semantic content, then that may be at least one reason why it can lead to a semantic paradox. (Note the irony of the adjective “semantic”.)

The first section deals with a purely syntactic logic as it applies to argument-forms. In the second section, Roger Penrose’s position on mathematical formalism is discussed in order to see if it can shed light on what may be deemed to be logical formalism. The third section deals with the syntax of premises (or sentences) mainly as they are found in logical arguments. It also comments on the philosophical consequences of dealing with premises (or sentences) in purely syntactical terms. The Final section pays exclusive attention to the “liar sentence” and defends the position that because it can be taken to have no semantic content at all (therefore it is treated purely syntactically), then that may be at least one reason why it leads to a paradox.

Empty Syntax

Noam Chomsky’s well-known example of a syntactically- and grammatically-correct surreal sentence.

The broad position of this piece is at least partly expressed by Stephen Read in the following:

“What must be acknowledged is that belief that every valid argument is valid in virtue of form is a myth, and exclusive concentration on the study of pure forms of argument does a disservice both to logic and to those who can be helped by it.”

That’s Stephen Read’s broad philosophy-of-logic position. And in the following piece a similar way of thinking is also applied to the premises (or sentences) actually found within arguments. 

Read then goes on the apply his (as it were) non-formalist position to the actual technical detail of valid arguments. He continues:

“Validity is a question of the impossibility of true premises and false conclusion for whatever reason, and there are arguments which are materially valid and where that reason is not purely logical.”

It can be argued that Read goes too far in the first passage above. That passage is a clearly a philosophical take on logic. Yet one can fully accept a purely syntactical (or formal) logic because such a thing clearly has its place. However, it’s also true — at least in part — that such a logic is indeed (to use Read’s words again) “a disservice to those who can be helped by it”. That is, for those interested in the philosophy of logic and in using logic in their philosophical arguments (i.e., logical arguments which aren’t about logic), the purely syntactical approach may seem odd or even pointless. On the other hand, syntactic (or formal) logic has had a great impact on metamathematics and mathematics itself. In addition, the purely formal way of looking at logic has been of great help to the development of programmes, computers and other technologies.

So one doesn’t need to reject syntactic (or formal) logic. One simply needs to accept that a purely syntactic logic is one thing, and a logic with important or relevant semantic content is another. Nonetheless, there’s more to it than that. If we recognise the important difference between syntactic logic and semantic logic, then that will help us explain much about the so-called semantic paradoxes and sentences like “This sentence is false”. (It may even help us develop a position on Gödel sentences.)

Stephen Read makes the formalist position on logic very clear when he states the following:

“Logic is now seen — now redefined — as the study of formal consequence, those validities resulting not from the matter and content of the constituent expressions, but from the formal structure.”

We can now ask: 

What is the point of a logic without material, semantic or relevant content? 

Wouldn’t all the premise, proposition, predicate, etc. symbols — not the purely logical symbols —used simply be self-referential in nature? (Thus all the p’s, q’s, x’s, F’s, G’s etc. would be autonyms.) And what would be left of logic if that were the case? Clearly we could no longer really say that it’s about argumentation at all— or could we? That is, we can still learn about argumentation from argument-forms which are purely formal in nature. The dots don’t always — or necessarily — need to be filled in.

Example

The following is both a valid and sound argument:

Football is a sport.
 — — — — — — —
∴ Snow is white.

To the layperson the above will seem both wrong and silly. However, classical logic allows premises and conclusions to be completely unrelated. That is, it is the form (hence argument-forms) of the argument that matters to logicians.

Now form is just as much a matter of premises (or sentences) as it is about arguments. As stated, the argument-form above is both valid and sound. But what of the premise (or antecedent sentence) itself? This premise is true. So is the conclusion. But what about this argument? -

This sentence is false.
 — — — — — — — — — 
∴ Football is a sport.

The premise above is perfectly acceptable — according to classical logic. The conclusion is also true. But is the premise also true… or false for that matter? If it is true, then the argument is valid. If it is false, then the argument isn’t sound. 

What if the premise is both true and false? Then, according to the principle of explosion, “anything and everything follows from it”. Thus the conclusion must also follow from it.

But what if the premise is neither true nor false, or both true and false? And what if its status as a proposition (i.e., as used as a premise) is questionable in the first place?

Roger Penrose on Formalist Mathematics

Roger Penrose and Plato.

A parallel to this issue of a purely formal logic can be found in mathematics — or at least in the philosophy of mathematics (or in metamathematics). For example, here’s the mathematical physicist and mathematician Roger Penrose on mathematical formalism:

“The point of view that one can dispense with the meanings of mathematical statements, regarding them as nothing but strings of symbols in some mathematical system, is the mathematical standpoint of formalism.”

Penrose has a serious problem with the “point of view” that is (or was) mathematical formalism. He goes on to say that “[s]ome people like this idea, whereby mathematics becomes a kind of ‘meaningless game’”. Penrose concludes:

“It is not an idea that appeals to me, however. It is indeed ‘meaning’ — not blind algorithmic computation — that gives mathematics its substance. Fortunately, Godel dealt formalism a devastating blow!”

One doesn’t need to be a Platonist to understand how formalism can also be a problem for logic. As it is, one can believe that both mathematics and logic can indeed have a purely formal aspect. Indeed one can see maths (though not logic) as always being purely formal (i.e., the contrary of Penrose’s position). However, in logic (unlike in mathematics) we have logical arguments expressed in a natural language. And these arguments contain sentences which include names and predicates. That is, they contain premises (or sentences) which have extensional, referential and existential import. None of this is true of maths — unless, that is, one believes that numbers, sets and even functions (as abstract objects) are the referents or extensions of numerals and other symbols!

Penrose on Mathematical Syntax

In the above the word “syntax” has been used a few times. So what exactly do I mean by the word “syntax”? Let Penrose again (though he’s talking about mathematics) explain:

“[‘S]yntactically correct’ essentially means ‘grammatically’ correct — i.e. satisfying all the notational rules of the formalism, such as brackets being paired off correctly, etc. — so that P has a well-defined true or false meaning.”

Indeed this “formalism” is given even more importance by Penrose because he places it within the context of David Hilbert’s quest for a systematic and secure grounding of all mathematics. Penrose continues:

“If Hilbert’s hope could be realized, this would enable us to dispense with worrying about what the propositions mean altogether! P would just be a syntactically correct string of symbols.”

Now Penrose rejects this formalism for mathematics. And here I am applying it to logic. Prima facie, if formalism can be challenged in the case of maths, then it seems to be far easier to challenge it when it comes to logic. After all, logic (among other things) makes explicit use of the words “true” and “false”. In addition, logic’s Ps and Qs are meant to stand in for propositions, which themselves can be (or are) expressed in natural-language sentences which contain names, predicates and suchlike. None of this can be found in maths. Indeed in maths the words “true” and “false” are rarely used in the symbolism itself. Any use of the words “true” and “false” that can be found are usually found in the domains of metamathematics and the philosophy of mathematics, not in mathematics itself.

So, as with logic, maths can be seen purely as a “game” (to use Penrose’s word just quoted above). Alternatively, maths can be given an interpretation or a philosophical account. Thus it can be said that formalists are like the shut-up-and-calculate brigade in quantum mechanics who’re only concerned with the mathematical formalism and how that formalism helps with experiments, predictions and observations. However, other physicists are also keen on the “interpretation” of quantum mechanics. That means that we can conclude by saying that Penrose is keen on the interpretation of maths. (His interpretation is essentially Platonic — see here.)

As for logic, rather than maths.

Robert S. Tragesser (who discusses Gottlob Frege) explains logical formalism in a similar way to which Penrose explained mathematical formalism. He wrote:

“Frege believed that the principle virtue of such formal-syntactical reconstructions of inferences — as validly moving on the basis of the meanings of the signs for the logical operations alone — was that it eliminated dependence on intuition and let one see exactly on what our inferences depended.”

The important point here being that it’s only “the signs for the logical operations alone” that have “meanings”. In other words, it doesn’t matter what conditions, events, facts, etc. A and B (in this case) stand for (or, in other cases, which natural-language sentences the symbols P and Q are meant to stand for), or what the conditional sign ⊃ “means” (i.e., beyond its syntactic role), what matters is the “formal-syntactical reconstructions of inferences” which (according to Frege at least) allow us to bypass any use of “intuition”.

The Logical Syntax of Sentences and Premises 

One problem with standard (or classical) logic is that the content of a premise is irrelevant. What matters is its form. So just as form is important in logical arguments, so form is also important when it comes to what are taken to be the premises (or sentences) found in logical arguments. This last aspect of logical formality hasn’t been discussed as much as the former.

Of course all premises are taken to have a semantics by formal logicians. If this weren’t the case, then they wouldn’t be seen to be premises at all. Yet the precise semantics isn’t the concern of the formal logician (if there is such a pure being). He doesn’t himself establish the references and extensions of the premises he uses. That is, premises are taken to have already-established extensions and references — otherwise they couldn’t be taken to be either true or false in the first place.

So logic always has a semantics or an interpretation.

In addition, there’s the (sorta) semantics of the symbols and their operations themselves. That is, a semantics of the symbols qua symbols and of the operations qua operations. In this case, the symbols and operations — taken in and of themselves — are taken to have “meanings”.

The heart of the problem can be seen when it comes to the logician himself. Specifically, it’s the distinction most (formal) logicians make between a sentence which is written down (or spoken), and the proposition that the written (or spoken) sentence is said to express. Such logicians are only interested in the proposition. Thus the proposition can be seen as being “underneath” or “behind” the sentence. Or, less metaphorically, the proposition is seen as being the idealisation of the sentence. 

This emphasis on the proposition is but a means to an end. Put simply, propositions are much easier to logically manipulate than natural-language sentences (as with sentences/statements which are given Gödel numbers).

All this will depend on what we take a proposition to be. And that may end up being partly — or even wholly — a stipulational matter. For example (as we shall see), it can be argued that if the sentence “This sentence is false” is without reference and extension, then perhaps it can’t be a genuine proposition at all. Having said that, in logic, it is taken to be a bona fide proposition.

The (as it were) formalist position on sentences (i.e., not on arguments) is put very well by Bryson Brown in the following:

“These rules are based on the syntactic structure of the sentences, that is the symbols and how they are arranged in each sentence, rather than on an account of their truth conditions.”

So here, rather than concentrate on the syntactic structure of an argument form, Bryson Brown talks of the “syntactic structure of a sentence”. In other words, the sentences (or premises) in this particular “consequence relation” can be seen as being purely syntactical too.

So why this stress on syntax? Bryson continues:

“One advantage of this approach to consequence relations is that it focuses our attention on the process of reasoning, rather than on ‘meanings’ that are taken to lie behind that process.”

This means that one can reason without a semantics; just as one can do arithmetic without worrying about the meanings — or the ontology — of the numbers one is using. 

So let’s tackle one logically-acceptable (though still philosophically problematic) sentence.

The Liar Sentence

The following is the liar sentence:

This sentence is false.

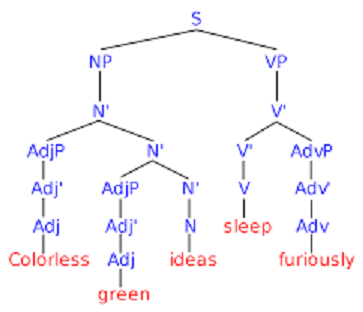
One problem is that the liar sentence certainly looks like other sentences. Grammatically, it appears to be in very good shape. It’s in good shape in a similar way to which Noam Chomsky’s well-known “colorless green ideas sleep furiously” (see image above) looks like a grammatically-acceptable sentence. (There are, of course, clear distinctions which can be made between the liar sentence and Chomsky’s surreal sentence.)

But what about the following? -

This sentence is true.

By inference, if one accepts the sentence “This sentence is true”, then one must also accept its negation — namely, “This sentence is false”. Yet it’s the case that the sentence “This sentence is true” is less problematic than the sentence “This sentence is false”. That is, the former doesn’t engender a paradox. Nonetheless, it’s still as empty as the sentence “This sentence is false”.

But firstly, let’s get something out of the way.

Take the liar sentence again:

This sentence is false. 

Is that really the logical form of the following? -

“All Cretans are liars.”

Aren’t there obvious differences between “This sentence is false” and “All Cretans are liars”? That may not matter because the former is still taken to be the logical form of the latter.

We can summarise the sentence “All Cretans are liars” in the following ways:

1) The sentence is spoken by a human person.
2) It includes the extension that is the set Cretan liars.
3) It is spoken by a member of the set Cretan liars.
4) It includes a reference to the psychological (behavioural) act of lying.

The sentence “This sentence is false”, on the other hand, has no extension or reference. So in what sense can it really be said to be the logical form of the sentence “All Cretans are liars”? If anything, the sentence “All Cretans are liars” is more acceptable than “This sentence is false” because the latter has no content and is paradoxical; whereas the former both has content and is paradoxical. 

Of course one can argue that the extension (or reference) of “This sentence is false” is the sentence itself (i.e., even if the sentence itself has no references or extensions). Thus the sentence “This sentence is false” can only have an empty inscription as its reference or extension. But an empty inscription can’t be a proposition (or statement). It’s a mere collection of words with an acceptable grammar or syntax. That is, a grammar or syntax without any semantic content.

Here’s another take. One possibility is that the sentence

“All Cretans are liars.”

should actually be something like the following:

“Except for myself, all Cretans are liars.”

The above is a more natural — and less problematic — expression of the words “All Cretans are liars”. However, the universal quantifier “all” ( or ∀ in logic) is negated by the proceeding clause “Except for myself”. This also has the consequence of making the entire sentence no longer paradoxical or self-contradictory.

Of course all this hinges on the quantifier “all” and the problems self-reference throw up. In logic, it’s often agreed that quantifiers nearly always have a restricted range (or domain) which is determined by specific contexts. Does that mean that the word “all” in “All Cretans are liars” also has a restricted range? Is the speaker of the words “All Cretans are liars” that very restriction (or exception) himself? Yet if we take the word “all” literally, then he can’t be. However, if we take the word “all” contextually or as a quantifier with a restricted range, then the Cretan liar may well be that very exception. After all, in natural-language terms (therefore also in terms of context), many people would be happy to accept that when a person says that “All people are evil”, then he may well be exempting himself from that universal generalisation. Indeed if someone were to say (out loud) that “All people always remain silent”, then (by definition) he must be an exception to his own universal generalisation.

Following on from all that, it’s also the case that the liar sentence can be seen as being neither true nor false. But here again it depends on which version we’re talking about. It seems easier to believe that the sentence “All Cretans are liars” is neither true nor false than the sentence “This sentence is false”. Why is that? Because it hardly makes sense to say of an empty sentence that it is neither true nor false. On the other hand, it makes more sense to say that the sentence “All Cretans are liars” is neither true nor false in that this may make sense of its paradoxical nature.

So there’s no actual truth-gap when it comes to the sentence “This sentence is false” because — arguably — the issue of truth or falsehood can’t arise in the first place for an empty sentence. Again, a truth-gap result may make much more sense for the sentence “All Cretans are liars” than it does for “This sentence is false”.

****************************

Strictly speaking, then, if any approach to logic is purely syntactical in nature, then truth and falsehood (at least as most people see such things) simply aren’t the issue. Having said that, if the symbols and operations in such a logic are correctly adhered to, then why can’t we call its results (or conclusions) “true” and “false”? After all, since what’s called “the nature of truth” has created controversy throughout the history of philosophy, then why can’t we be a little logically ad hoc about this matter?