Dr Christoph Schuringa Demands That Analytic Philosophy Become Political

 

i) Introduction

ii) Everything is Political: Therefore Analytic Philosophy is (“Unwittingly”) Political

iii) The Politically Suspect Identity of Analytic Philosophy

iv) Conclusion: Analytic Philosophy is Capitalist

The following is a response to a piece called ‘The never-ending death of analytic philosophy’, by Dr Christoph Schuringa.

Despite the mention of “death” in his title, Schuringa goes on to tell us that

“analytic philosophy somehow seems to continue to be with us as the dominant force in academic philosophy”.

Christoph Schuringa has written a lot on Karl Marx. So perhaps Marx’s own well-known words against philosophy may well sum up Schuringa’s own position on analytic philosophy. Indeed there’s even a reference to “Marx on the ‘supersession’ of philosophy” on Schuringa’s academic webpage (see screenshot below).

In his Theses on Feuerbach, Marx wrote:

“The philosophers have only interpreted the world in various ways; the point, however, is to change it.”

So is Schuringa attempting his very own supersession of analytic philosophy?

Well, it’s certainly the case that Schuringa wants to change analytic philosophy — radically! Whether Schuringa also believes that philosophy’s main — or even only! — goal is to change the world will hopefully become clear in the following.

As for biographical details, let Christoph Schuringa speak (or write) for himself:

“I am Assistant Professor in Philosophy at the New College of the Humanities (part of Northeastern University), and Editor of the Hegel Bulletin. My chief interests are in the history of philosophy (especially Kant, Hegel, and Marx), in the traditions of Marxism and critical theory, and in social and political thought more widely. Specific current research projects concern Marx’s critique of Hegel, the concept of Gattungswesen, and ‘tragic’ conceptions of philosophy. My large-scale current project is a monograph I am writing on Marx… I was recently in the Philosopher’s Zone (ABC Radio National, Australia), talking about the history, and prospects, of analytic philosophy (broadcast 20th June 2021).”

This is Christoph Schuringa advising Sky News viewers to read Marx (view here).

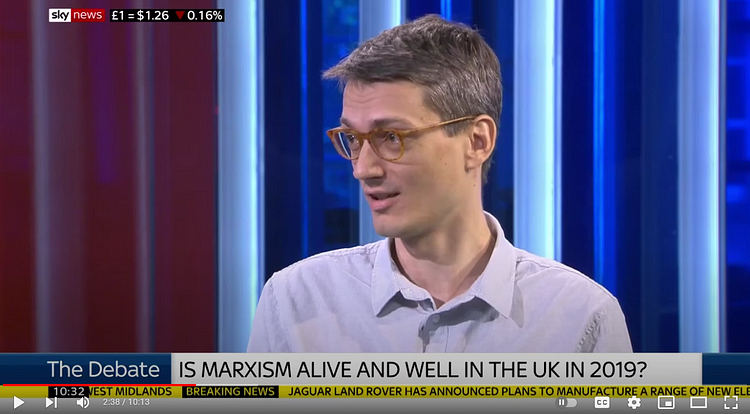
As you can see, there’s not much analytic philosophy above — save for the final bit about “talking about the history, and prospects, of analytic philosophy”. So Schuringa is essentially “talking about” analytic philosophy from the outside. (Although Schuringa might well have been “trained” in analytic philosophy.)

It can also be seen that in Schuringa’s ‘Selected Publications’ (screenshot above) there’s no analytic philosophy there either. (The one exception is The Act and Object of Judgment: Historical and Philosophical Perspectives — a book Schuringa edited but didn’t contribute to.)

So Schuringa has basically declared war on analytic philosophy from the outside. This is not, then, a civil war initiated by someone who finally came to see the limitations of — and problems with - analytic philosophy after years of writing and teaching it (say, as Richard Rorty did).

Everything is Political: Therefore Analytic Philosophy is (“Unwittingly”) Political

Rebecca Solnit’s words are almost identical to Christoph Schuringa’s own — as quoted below. (Solnit, like Schuringa, is a writer, political activist and anti-capitalist.)

To Dr Christoph Schuringa, it’s literally all about politics.

As Schuringa says of a previous period of analytic philosophy:

“[T]he philosophical work [of analytic philosophers] remained untainted by politics.”

That statement statement basically contradicts other words by Schuringa in that to be “untainted by politics” (or to be “apolitical”) is actually to be political (see later). That said, to be untainted by politics is still a serious problem for Schuringa.

So why did Schuringa feel the need to talk about “the death of analytic philosophy” in the first place?

It can easily be shown that Schuringa desires (or wants) the death of analytic philosophy.

Of course Schuringa will deny that because it’s simply too extreme to put it in that absolutist way. Instead, he’ll probably argue that he simply wants to change (à la Marx) analytic philosophy.

Yes; Schuringa does want to change analytic philosophy — to radically change it. To change it in very specific political ways. Indeed to change it so radically that — it can be argued — it would no longer be analytic philosophy at all once all the changes Schuringa wants were carried out.

And if all this were to happen, then analytic philosophy will be yet another academic discipline — like the Critical Race Theory Schuringa positively cites — devoted entirely to political change.

What a miserable one-dimensional academic and intellectual world Schuringa wants. Indeed it can be wondered if he also has strong political problems with non-political art, music, physics, biology, mathematics, etc.

It’s not a surprise, then, that Schuringa barely conceals his anger (despite the controlled academese) that

“analytic philosophy somehow seems to continue to be with us as the dominant force in academic philosophy”.

Yet there’s also a lot of history in Schuringa’s article — all solely cited to (as it were) prove his political point.

So it seems that Schuringa is largely a historian of philosophy. He displays his historical scholarship in the following words:

“Analytic philosophy was once (in the 1950s) a strident, crusading movement. Having been constituted by Feigl and Sellars, and others, it quickly gained control of American philosophy departments.”

All I can say is that I’ve lost track of the many times I’ve read and heard people’s words against analytic philosophy which have been expressed in an extremely “strident” manner. Moreover, some of those strident voices in the past (as Schuringa tells us) moved away from (analytic) philosophy departments and “quickly gained control of [other humanities] departments” which weren’t explicitly devoted to philosophy.

In other words, were these academics pushed out of American philosophy departments (by analytics) or did they willingly decide to move? That is, did they take a mainly political (i.e., not philosophical) position (like Schuringa himself) against the lack of political activism in — and the lack explicit political commitment from — these philosophy departments and then decide to move elsewhere? Alternatively, perhaps there was a mixture of pushing and willingly moving.

In any case, it seems that people with very similar political views (to the ones who who “gained control” of many humanities departments) are still not happy that analytic philosophy so much as exists — despite the numerous departments which offer something very different.

Yet Schuringa still wants the death of analytic philosophy!

He also wants a political hegemony in philosophy departments which is much more loyal to his own personal politics.

And, again, Schuringa mentions analytic philosophy’s “strident opposition to alternative approaches to philosophy” without bothering to mention the strident opposition to analytic philosophy which has been displayed by many continental philosophers (including Jacques Derrida), political theorists, political activists, etc. Indeed, underneath the polite and (seemingly) careful academese, I would happily say that Schuringa is stridently against almost all analytic philosophy. (Check out his publications for evidence of that.)

Schuringa is also explicit in his political analysis of analytic philosophy; as well as in his view that it was always — if only by default (or “unwittingly”) — political anyway (as already mentioned). He writes:

“[T]he ‘apolitical’ are, just by virtue of sealing themselves off from political engagement, particularly susceptible to unwittingly falling into line with the prevailing ideology and its structures.”

This is a classic expression of an endlessly-repeated Marxist trope. Here goes:

If one is apolitical, then one is political.

Or:

If one is anti-political, then one is political.

Pointing this out will lead many people on the Radical Left to question my “naïve” and “unsophisticated” bifurcation of philosophy and politics (Schuringa will certainly do so) — and that in itself will be a political position. This was the traditional Marxist response to all people who put the view that there are at least some domains that simply aren’t political — at least not in any clear or non-questioning-begging sense.

This complete denial — or rejection — of any separation of philosophy (or anything else for that matter) from politics has, of course, become de rigueur and hugely widespread in various domains in the last 30 years or longer — especially in many British and American university departments. Indeed the embracing of the idea that “everything is political” has given activists like Schuringa the perfect excuse to make everything political. That means that there’s nothing to hold such academics back once they embrace the essentially Marxist catechism that everything is political… even a lump of dogshit or the “idea of a quark”.

Yet this back and forth between stating that analytic philosophy isn’t political (or isn’t political enough) and saying that it was always political anyway leads Schuringa to state the following:

In order for analytic philosophy to “develop and grow”, it most become political in only radical ways.

… ways which just happen to perfectly square with Schuringa’s own personal politics.

Schuringa is explicit about his political demands when he writes the following words:

“It will not be enough to regiment some of the ideas in, say, critical race theory, extracted from another literature using its own procedures and on its own terms, into its own format.”

In other words, an analytic-philosophy version of Critical Race Theory (if such a thing could ever exist) simply wouldn’t be enough for Schuringa. He demands a literal Critical Race Theory (i.e., from analytic philosophers) which hasn’t been (politically) watered down with the tools, methods and standards of analytic philosophy. That is, he wants an analytic philosophy that has

“open[ed] itself to immersion in cultural, social and political reality”.

… But only an immersion that perfectly squares with the theories, values and goals of Schuringa’s personal politics.

All this is Schuringa’s roundabout — and academic — way of saying that analytic philosophy must become a weapon of social and political change. That is, it must actually stop being analytic philosophy and become something entirely different. More specifically, analytic philosophers must become exactly like those legions of Critical Race Theorists, Marxists, post-structuralist philosophers, postmodernist philosophers, etc. who basically believe — and have believed for the last six decades or so — that politics must always be First Philosophy.

So Schuringa’s political plan isn’t simply about making analytic philosophy more politically (or socially) aware. It’s about making analytic philosophy more aware of the political theories, causes and goals that Schuringa himself has thoroughly embraced — both in his academic work and in his non-academic activities.

For example, Schuringa writes:

“[Analytic philosophy] has heard the call of feminism, of critical race theory, and of the movement to decolonize the curriculum, and it is actively in the business of trying to heed these calls.”

As with Schuringa’s remarks on Critical Race Theory above: it’s simply not enough to “hear[] the call” of feminism, Critical Race Theory and the movement to decolonize the curriculum: analytic philosophy must become as one with all of them.

Schuringa even tells us about what analytic philosophy may become once it has completely embraced and faithfully enacted every letter of his political plan (then politically redeemed itself). He writes these pompous words:

“[Analytic Philosophy] will then have the prospect of being, for the first time, truly alive.”

So “truly alive” simply means being truly and correctly political.

Actually, it’s even more concrete than that: “truly alive” simply means being truly political in ways which Schuringa agrees with.

So the politicisation of analytic philosophy is not only what Schuringa demands. He also demands the politicisation of analytic philosophy in only his ideologically-correct ways. Hence Schuringa’s very specific and very positive references to Critical Race Theory, “the decolonisation of the curriculum”, etc.

[A quick aside: All this is very odd from a personal — social media — point of view too. In terms exclusively of Twitter: almost — or even literally — every analytic philosopher I “follow” and know is on the Left — from the Radical Left to the “centrist” or “liberal” Left. (There is a very-very small number of analytic academics who may well be Liberal Democrats — but they also lean to the Left. Not a single one is a Tory or right-wing in any sense — though more-Left-than-thou activists may disagree about that.) What’s more, many of these analytic philosophers on Twitter openly and explicitly express their leftwing views and do so very often. Indeed a small number of them could even be classed as political activists… All that said, Schuringa would — or could — simply argue that although these philosophers are indeed on the Left, what they do — i.e., analytic philosophy — most certainly isn’t!]

The Politically Suspect Identity of Analytic Philosophy

Schuringa then psychoanalyses analytic philosophers. He tells us that

“[i]t might be thought that analytic philosophers have experienced a healthy (and mild) identity crisis”

in that they might — or should — have

“come to see that they have much in common with other approaches, so are less inclined to insist on their own identity”.

Yet, on the whole, Schuringa believes that most (or all) analytic philosophers certainly haven’t done this.

Schuringa has a problem with the “identity” of analytic philosophy… Basically, that it so much as has one.

Take the following words:

“An object lesson in the tendency of analytic philosophy to mark itself out as distinctive from the rest of philosophy is the divide that it created between itself and what it called ‘continental philosophy’.”

Yet it seems that Schuringa doesn’t have a problem with Critical Race Theory, feminism, etc. having their own identities. I suspect that he doesn’t have a problem with university departments specialising in Marxism, post-structuralism, Black Studies, etc. having identities either. Indeed I also suspect that he’s also very much in favour of “identity politics” too (though, of course, he’ll reject that term).

Schuringa says more about the identity of analytic philosophy. He wonders if

“there was ever a unified kind of philosophy called analytic philosophy”.

A philosopher may have a commitment to analytic philosophy without thinking too much about it. (Schuringa seems to argue that analytic philosophers both are and are not self-conscious about what they do.) After all, since a fair few non-analytic philosophers are keen to stress analytic philosophers’ complete ignorance of the history of philosophy (which Schuringa himself is attempting to rectify in his article), then this degree of historical self-consciousness among analytic philosophers won’t exist to any strong degree.

If we get back to his Schuringa and the identity of analytic philosophy.

Now every university faculty on the planet has its own focus and specialisms — such as Black Studies or much of what’s studied at the University of London School of Oriental and African Studies. Yet, according to Schuringa, this rejection of continental philosophy, Critical Race Theory, etc. is deeply suspect. So should the UK and US departments which concentrate on, say, Subaltern Studies also be more inclusive — should they also run a few courses on Hayekian economics or modal logic? Or, more relevantly, should philosophy departments which concentrate on what’s called Continental Philosophy broaden their own horizons by allowing in professors who are experts on the analytic philosopher Ted Sider, the (analytic) philosophy of science or the (analytic) philosophy of mind?

Moreover, there are countless university departments which offer “studies” which advance the political causes Schuringa believes in. Indeed some of them can even be vaguely construed as doing various kinds of (politically-committed) philosophy. Now is analytic philosophy really a rival — let alone any kind of political threat — to all the following? -

Black Studies, Social & Cultural Analysis, Post-Colonial Studies, Subaltern Studies, Deconstruction, Critical Race Theory, Global Liberal Studies, Ethnic Studies, Africana Studies, Cultural Studies, Gender and Sexuality Studies, Literary Theory, Peace and Conflict Studies, Feminist Geography, Discourse Analysis, Africana Studies, etc.

To add to the above it’s worth mentioning the fact that there was even a Centre for Contemporary Cultural Studies at Birmingham University which explicitly committed itself to what it called “cultural Marxism”. (Now that non-Marxists have caught onto the term “cultural Marxism”, Marxists rarely use it anymore - see here.) And there’s the New School for Social Research in New York which is devoted to teaching what it calls “progressive values”. (This “school” wouldn’t even allow a young student in if he/she had the wrong politics — not that such a person would attempt to gain entry in the first place.) There are many other educational institutions like this — a small number are on the Right too. Yet all these institutions are far more politically biased — indeed openly and blatantly so! — than any analytic philosophy department has ever been. That said, Schuringa actually endorses such political bias — or “political commitment” — in such institutions (if only bias of certain political kind).

In fact the studies (or the academics who teach and advance them) mentioned above rule the roost in many American university departments and even in the entire universities themselves.

More generally, it must also be said that literally all disciplines are isolated from other disciplines… to some degree. This is true of literary theory, poststructuralism, Critical Race Theory, history, anthropology, etc. It’s certainly true of physics, chemistry, etc. In fact it can be argued that that’s partly what makes a discipline a discipline — a degree of isolation from other disciplines. That said, almost every analytic philosopher I know — both throughout the 20th century and today — did have a keen interest in other disciplines such as physics, biology, ethics, neuroscience, mathematics, etc. And, more recently, in cognitive science.

It’s also worth adding here that it’s not just that Schuringa wants analytic philosophy to fully embrace Critical Race Theory, continental philosophy, etc., he also believes that it should embrace non-European thought too.

So once wonders what would be left of analytic philosophy after Schuringa’s political and academic Year Zero.

The following is Schuringa on the particular subject of non-Western thought:

“Philosophy as a discipline has a huge whiteness problem, and it is right that the hegemony of Western philosophy in the academy must be addressed if the curriculum is to be effectively decolonized.”

In this, Schuringa is adopting a similar position to Professor Bryan Van Norden. Indeed Van Norden once wrote an essay called ‘Western Philosophy is racist. In that essay he wrote the following:

“Mainstream philosophy in the so-called West is narrow-minded, unimaginative, and even xenophobic.”

Again, what would be left of analytic philosophy — or even “Western philosophy” — if these academic activists got their way?

Like Schuringa himself, Professor Van Norden’s case against Western philosophy is almost entirely political. Indeed he lays his own political cards on the table when he calls his position “a multicultural manifesto”. And whereas Schuringa suggests Critical Race Theory, etc. as an antidote to the political sins of analytic philosophy, Van Norden wants analytic philosophers to study

“African-American, Christian, feminist, Islamic, Jewish, Latin American, and LGBTQ philosophies”.

Conclusion: Analytic Philosophy is Capitalist

Schuringa does acknowledge that there has been at least some change when it comes to analytic philosophy … just nowhere near enough to please him. He writes:

“And so what we are left with is a more modest kind of analytic philosophy — a modesty perhaps reflected in a less strident opposition to alternative approaches to philosophy among analytic philosophers today.”

The assumption here is that if analytic philosophy becomes political (despite it already being apolitically political), then it must become political in very particular ways. And if it does become “more sensitive to the other”, then it must be more sensitive to the very particular others Schuringa himself has in mind.

Schuringa can’t even resist some explicit and classic Marxist politicking when he states the following:

“[A]nalytic philosophy tends to conceive debate on the liberal model of a ‘marketplace of ideas’…… The problem with the marketplace of ideas, as with the commercial marketplace of classical and neoclassical economics on which it is modelled, is that it treats each participant in the marketplace as de facto engaging in exchange on equal terms.”

[Schuringa argues against what he calls “liberal democracy” — as well as against capitalism, the “founding fathers”, etc. — here. See screenshot left.]

So this isn’t really about philosophy or even about Richard Rorty’s analytic “style”. It’s not about the critical emphasis on logic, “scientism” and all the other sins of analytic philosophy either. It’s really about

“this whole conception of equal engagement stands in need of critique”.

And that’s why there’s hardly a word on what analytic philosophers have argued or believed in Schuringa’s article except from a self-consciously historical point of view — all designed to show how variable analytic philosophy has actually been. (Doesn't that fact actually work against much of what Schuringa says?) In other words, there’s virtually no philosophy in the article; though there is lots of history of (analytic) philosophy. Yet that historical research itself is only a tool to advance Schuringa’s central political aims.

Schuringa’s sees everything through a political lens.

He simply doesn’t do philosophy or engage with analytic philosophy at all. And that primarily because all (non-political) philosophy — as Marx argued 170 years ago — is by definition suspect or fallen. Thus analytic philosophy itself must redeem itself by committing itself to a very specific kind of politics — radical politics.

So unless analytic philosophy gets its act together and becomes politically activist (in the ideologically-correct manner, of course), then it will remain the case that

“the very ideas of feminism and critical race theory are deprived of their very point and rendered impotent if discussion takes place on these terms”.

This is like the Marxist idea that literally all criticisms of Marxism are the result of “false consciousness” or of being a member of the enemy class. Yet once you make the absolute and complete leap of faith into Marxism, then you will see that Marxism is the Truth and that all one’s previous criticisms were result of “class bias”, “brainwashing by the mainstream media”, political sin or whatnot.

Similarly with Schuringa’s Critical Race Theory, etc.

Analytic philosophers mustn’t — or can’t — simply take on board Critical Race Theory or even embrace many aspects of it. Instead, they must fully embrace it in thoroughly activist sense. (In the sense that Schuringa himself uses philosophy as a political weapon.) Because if analytic philosophers don’t do what Schuringa demands, then (among other things) “the very ideas of feminism and critical race theory are deprived of their very point and rendered impotent”.

So analytic philosophy must simply stop being analytic philosophy.

It must become a philosophy of political activism.

Indeed it must commit itself to very specific political theories, causes and goals and also to very specific political movements — all those which just happen to be endorsed by Schuringa himself.

One may ask, then, what would be left of analytic philosophy were Schuringa’s many absolutist and all-encompassing political demands ever met.

Nothing would be left.

Quite literally — nothing.

[I can be found on Twitter here.]

Lee Smolin Deflates the Tacit Pythagoreanism of Today’s Physicists

 

“The distinction between science and mathematics had only been clarified in the late nineteenth century. Until then it might be supposed that mathematics necessarily represented the relations of numbers and quantities appearing in the physical world, although this point of view had really been doomed as soon as such concepts as the ‘negative numbers’ were developed… Mathematical symbols became less less and less obliged to correspond directly with physical entities.”

— Andrew Hodges (in Alan Turing: The Enigma)

[The image above is taken from Lee Smolin’s book The Trouble With Physics. However, none of the quotes in this essay are from that book - they’re mainly from his The Life of the Cosmos. That said, this essay does highlight what Smolin takes to be the trouble with physics.]

The American theoretical physicist Lee Smolin (1955-) argues that the belief in the intrinsically mathematical nature of Nature (or reality) “is the private religion of the theoretical physicist”. Smolin’s words can be taken to be hinting at a contemporary kind of Pythagoreanism when it comes to such physicists. And, of course, it’s a historical fact that the early — as well as later — followers of Pythagoras (c. 570 — c. 495 BC) were members of various religions or (depending on one’s views) cults (see here).

The Unreasonable Effectiveness of Mathematics

Lee Smolin refers to “the obvious effectiveness of mathematics in physics”. That is a statement about the pragmatic utility of mathematics when it comes to physics. Or, to use Eugene Wigner’s oft-quoted words, Smolin is basically referring to “the unreasonable effectiveness of mathematics in the natural sciences”.

We can all happily accept the unreasonable effectiveness of mathematics in physics.

But where do we go from there?

Smolin himself goes on to state that he has

“never heard a good a priori argument that the world must be organised according to mathematical principles”.

So Smolin has “never heard a good a priori argument” on this subject - despite the obvious effectiveness of mathematics.

Again: mathematics is useful — extremely useful — in physics. So much so that there could hardly be any modern physics without maths. That said, it still can’t be concluded from this effectiveness that (to use Smolin’s words again) “the world must be organised according to mathematical principles”.

In other words, the unreasonable effectiveness of mathematics doesn’t mean — or have the consequence — that the world itself is [or must be] organised according to mathematical principles. Of course it gives physicists reasons — even very good reasons — to believe that. However, the effectiveness of mathematics in physics — alone — doesn’t have the (logical) consequence that the world itself must be organised according to mathematical principles.

More specifically, when Smolin uses the words “a good a priori argument” (or simply when he uses the epistemological term “a priori”) he seems to be saying that many physicists simply assume that Nature is mathematical precisely because of the unreasonable effectiveness of mathematics in physics… or, indeed, vice versa.

So this is close to being a circular position. Thus:

(1) Mathematics is unreasonably effective in physics because the world itself is mathematical. 
(2) Because the world is mathematical, it follows that the mathematics in physics will be unreasonably effective.

Later in the same chapter Smolin goes on to be even more explicit about these assumptions when he writes the following words:

“[W]hat is both wonderful and terrifying is that is absolutely no reason that nature at its deepest level must have anything to do with mathematics.”

At first sight, this seems like an incredible claim.

Or at least one would presume that most — or even all — physicists would have (deep?) problems with Smolin’s statement. But that shock may — again - simply be down to the false inference (which many physicists make) from the the unreasonable effectiveness of mathematics to the conclusion that nature itself (“at its deepest level”) must be mathematical.

To repeat: we have the following line of reasoning from mathematical and theoretical physicists:

(1) Mathematics is unreasonably effective in physics. 
(2) Therefore the world itself must be organised according to mathematical principles.

(Not that all or even most physicists actually express — or even think about — these issues.)

But isn’t the above like making the following (admittedly much weaker) claim? —

(1) Cement is unreasonably effective when it comes to building houses. 
(2) Therefore houses must be built on cement-based principles.

Pythagoreanism or Platonism?

Pythagoras… or Plato?

The distinctions that shall now be made between Platonism and Pythagoreanism may be mere semantics. I say that because they may only amount to differences which don’t really make (much of a) difference.

But here goes.

Platonists stress the abstract world of mathematics and its complete separation from what’s often been called “the sensible”. On this reading at least, that would mean that mathematical and theoretical physicists gain hold (or, to use Roger Penrose’s word, “see”) these “perfect mathematical form[s]” in Plato’s domain, and then they simply make use of them to describe, explain or even (to use Smolin’s word) “mirror” Nature.

Pythagoreans, on the other hand, believe that such perfect mathematical forms are actually instantiated in nature — not a mere “reflection” of anything in the Platonic realm.

Thus Platonists have traditionally played down the sensible world and stressed the abstract world of mathematics. Pythagoreans, on the other hand, have discovered mathematics — and even “perfect forms” — within nature itself and thus never felt polluted by investigating (sensible) Nature.

Plato’s overall philosophy can also be read as not being primarily about numbers; whereas Pythagoras’s philosophy (or religion) was. That is, Pythagoras was far more concerned with showing the mathematical nature of the world (or Nature) than Plato. For Plato, indeed, mathematics has its own abstract world — which the physical world merely “copies”.

Thus it is easier to note a Pythagorean position in mathematical and theoretical physics than in pure mathematics. Similarly, it’s easier to note a Platonic position in pure mathematics than in mathematical and theoretical physics.

Despite all that, I must freely admitted that I’m not a scholar of either Plato or Pythagoras. Thus what I argue may only be a case of my own personal take on the two philosophers. So, even if my interpretative distinctions between Platonism and Pythagoreanism are incorrect, the distinctions I make are still real and — I believe — they still make a difference. Again: that’s the case even if my distinctions don’t accurately capture the actual historical differences between the two philosophers.

To put all that in very basic terms: I’m not a historian of philosophy.

Smolin’s Own Position on Pythagoreanism & Platonism

In the words above there was an attempt to make a distinction between Platonism and Pythagoreanism. And Smolin himself also gets to the heart of the issue of the relation between mathematics and reality — as it relates to both Platonism and Pythagoreanism.

To use Smolin’s own words to put the mathematical Platonist’s position: “appearances” are deceptive — even in physics. They’re also thoroughly contingent. So what underlies our physics is a “transcendent reality” — and that reality is entirely (or purely) mathematical.

Of course Plato famously warned us against accepting (mere) appearances. Yet Smolin’s words aren’t only about the appearances Plato warned us against.

Smolin — as I read him — is also referring to appearances as they’re found in physics itself. That is, Plato warned us — in his famous allegory of the cave — against taking the shadows on the walls to be real beings (or things). Yet the position Smolin is tackling has it that even the physical properties, events, etc. mentioned in physics are themselves stand-ins for the mathematics which underpins them.

So this means that laypeople can be just as easily fooled by the appearances offered by physicists as the prisoners in Plato’s allegory were fooled by the shadows on the wall.

That said, one problem is that Smolin seems to (more or less) fuse Plato and Pythagoras. Take the following example. Smolin writes:

“From Pythagoras to string theory, the desire to comprehend nature has been framed by the Platonic ideal that the world is a reflection of some perfect mathematical form.”

It can be argued that contemporary Pythagoreans would say that mathematics is actually instantiated in nature rather than our mathematical physics being (merely) “a reflection of some perfect mathematical form”. Pythagoreans may even argue that (as with Pythagoras himself) “the world is number” — as does, for example, Max Tegmark (see here). Indeed Smolin himself comments on that (supposed) literal identity between “reality” and mathematics when he mentions what he calls “[t]he mysticism of the mathematical”. He writes:

“[T]he belief that at its deepest level reality may be captured by an equation or a geometrical construction [].”

Yet it can also be argued that Smolin’s word “captured” works against Pythagoreanism in that saying that “an equation” captures an aspect (or part) of “reality” doesn’t appear to be the same thing as saying that an aspect (or part) of reality instantiates — or literally is — an equation. (Max Tegmark actually holds this position.)

Then there’s also another passage from Smolin which works against a purely Pythagorean reading. Smolin has it that

“the ambition then rises in our young scientist that he or she may be the one who invents the formula that is the true mirror of the world”.

Surely it would be the case that for a Pythagorean his mathematical “formula” wouldn’t be “the true mirror of the world” — it would be the world. That it, the formula would either be instantiated in the world or there would be a literal identity between formula and the world. Smolin’s words, therefore, chime in better with Platonism in that the physical world is seen to “mirror” (if often badly) the mathematics of Plato’s abstract world.

What’s more, how exactly could a mathematical formula “mirror the world”?

Consider here the many problems philosophers have noted with the (supposed?) “correspondence” between statements (or sentences) and facts; as well as the referential problems brought about by words and what words refer to or name. (See the Correspondence Theory of Truth.) Now is the mirroring of the world by formulas (equations) really that different? More relevantly, what is the precise relation between a “perfect mathematical form” in a Platonic realm and a physical part of the world?

As for reality being captured by an equation or a (to use Smolin’s words) “geometrical construction”.

It can now be said that even Stephen Hawking (1942–2018) came to argue (in the years just before his death) against the possibility of (to use Smolin’s words) “some [single] beautiful mathematical structure that will underlie reality”. Or, more accurately, since Hawking came to argue against the possibility of any “theory of everything”, then it would have been even more likely that he’d never have believed that there could be a single beautiful mathematical structure which described (summed up, “mirrored” or whatever) literally everything.

What would that even mean?

(This line of reasoning can be found in Hawking’s book The Grand Design and in the article Stephen Hawking says there’s no theory of everything | New Scientist.)

More specifically, even short — yet still powerful and wide ranging — equations are only short because they contain within them large amounts of tacit, implicit or simply missed out mathematical and physical information. Or, to put that differently, a short — yet still powerful and wide ranging — equation actually contains within it many other equations — most of which are represented by single symbols.

So, when you take this line of reasoning to its limit, then it’s no surprise that we could (to adopt and adapt a quote from The Hitchhiker’s Guide to the Galaxy) accept that “the answer to Ultimate Question of Life, the Universe, and Everything” is indeed the number 42!

Despite all the above, Smolin still hints at what can be taken to be the Pythagorean beliefs of many mathematical and theoretical physicists. He writes:

“Certainly, if one needs to believe that beyond the appearances of the world there lies a permanent and transcendent reality, there is no better choice than mathematics.”

The problem Smolin is highlighting (as already mentioned) is this:

(1) If one believes in the unreasonable effectiveness of mathematics in physics, 
(2) and then moves from (1) to also believing that the world is organised according to mathematical principles,
(C) then it seems logical to conclude that the world itself is mathematical.

After all, if you have the efficacy of maths, along with the belief (or even fact) that the world (as it were) obeys mathematical principles, then it’s a (fairly) smooth ride from those positions to endorsing (even if only tacitly) some kind of Pythagoreanism.

Smolin’s Maths-to-World Examples

Smolin explains the strange and strong link between mathematics and the physical world — as well as the independence of mathematics — when he cites the case of

“a beautiful piece of mathematics [which was] first explored simply because it was beautiful, but later was found to represent a real phenomenon”.

Smolin then provides some examples of this phenomenon:

“This is certainly the story of non-Euclidean geometry, and it is the story of the triumph of the gauge principle, from its discovery in Maxwell’s theory of electrodynamics [].”

And, elsewhere, Smolin writes:

“The power of this dream is undeniable, as we can see from the achievements it inspired, from Kepler’s laws to Einstein’s equations. Their example suggest that the goal of theoretical physics and cosmology should be the discovery of some beautiful mathematical structure that will underlie reality.”

For a Pythagorean, however, that “beautiful piece of mathematics” wouldn’t “represent a real phenomenon”: it would actually be instantiated in (or even be) that real phenomenon.

A Platonist (at least on this reading), on the other hand, would luxuriate in the beauty of this piece of mathematics as it is in itself — without any wish to make is represent a real phenomenon. Indeed one can cite that supreme Platonist mathematician G.H. Hardy (1877–1947) here. Hardy would have been outraged had “some tiresome physicist [] come along and found a use for [his equation]”. Indeed Hardy once stated the following words:

“I have never done anything ‘useful’. No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world.”

Surely Hardy’s expressions above aren’t those of a Pythagorean because “the world of numbers”, the applications of mathematics (in physics and elsewhere) and indeed ethics were all very important to Pythagoreans. Mathematical Platonists like Hardy and others (if not Plato and Platonists generally), on the other hand, tend to have a much more rarefied view of these matters.

Smolin’s Darwinian and Wittgensteinian Philosophy of Physics

“[N]ot much of what happens in the natural world is governed in a systematic way, that it takes an enormous amount of effort in special background conditions in special circumstances before you get regular repeatable behaviour.”

— Nancy Cartwright (1944-) (see here)

One may now be wondering what Smolin’s own overall philosophical position is on the matters discussed above.

So take the following words:

“Each atom moves randomly, it is just the statistics of enormous numbers. Perhaps the greatest nightmare of the Platonist is that, in the end, all our laws will be like this, so that the root of all the beautiful regularities we have discovered will turn out to be more statistics, beyond which is only randomness or irrationality.”

That position on physics seems to be somewhat Darwinian in nature. That’s because the passage above emphasises randomness (as also in random mutations) leading to regularities (as also to determinate — at least for a time — species). That’s not a surprise because Smolin takes a Darwinian position on other elements in physics. It’s worth noting, then, his best known — and seemingly bizarre — Darwinian position on blacks holes and the nature of (in the plural) universes.

Smolin’s hypothesis is one of cosmological natural selection. In very basic terms, Smolin argues that a process similar to biological natural selection occurs at the cosmological scale. More specifically, Smolin argues that it is black holes which have a role in cosmological natural selection. That is, black holes give birth to new universes. These new universes have fundamental constants whose “parameters” may differ — if only slightly — from those of the universe in which the black hole collapsed. This also means that every universe will produce as many other universes as it has black holes.

And all this ties in with the evolutionary ideas “mutation” and “reproduction” — yet applied to black holes and their progeny (i.e., universes).

If we return to Smolin’s account of Platonism directly above.

There’s a certain degree of rhetoric in that passage. That is, I wouldn’t say that any element of “each atom” displays “irrationality”… or, for that matter, rationality. Indeed the Dutch philosopher Spinoza (1632–1677) once wrote the following words of warning about this anthropomorphic way of thinking:

“I would warn you that I do not attribute to nature either beauty or deformity, order or confusion. Only in relation to our imagination can things be called beautiful or ugly, well-ordered or confused.”

That said, Smolin may simply be expressing a Platonist way of looking at (in this case) atoms.

Now take some more Darwinian words from Smolin:

“This is perhaps one reason why biology seems puzzling to some physicists. The possibility that the tremendous beauty of the living world might be, in the end, just a matter of randomness, statistics, and frozen accident stands as a genuine threat to the mystical conceit that reality can be captured in a single, beautiful equation.”

[On the term “frozen accident” above: “The Frozen accident hypothesis assumes that the formation of the genetic code is an example of a frozen accident (Crick 1968) [] the genetic code was formed through a random, highly improbable combination of its components formed by an abiotic route…]

Here again we read Smolin referring to that “single, beautiful equation” which Stephen Hawking had doubts about. However, a Pythagorean theoretical physicist like Michio Kaku (1947-) is always dreaming of such of thing and very frequently mentions it. Indeed one suspects that Kaku believes that it may be himself that creates (or discovers) the equation. And that may at least partly explain why he’s written a book called the God Equation. (Won’t the discoverer of the God Equation be… God-like?) Indeed, according to Kaku himself, he’s been searching for a “theory of everything” since he was 8 years old.

In any case, although Smolin’s position on much of physics is Darwinian, his position on (pure) mathematics appears to be Wittgensteinian.

Wittgenstein

For an example of this, take the following very Wittgensteinian passage from Smolin. (I’ve no idea if Smolin has been influenced by Ludwig Wittgenstein because I only recall him writing about the Austrian philosopher on one occasion — here.) Smolin writes:

“Like mathematics itself, the faith in this shared mysticism of the mathematical scientist is an invention of human beings.”

Here Smolin explicitly states that “mathematics itself [] is an an invention of human beings”. This means that if maths is an invention of human beings, then there’s no reason at all to assume that reality (or the world) is intrinsically mathematical — let alone that equations (or formulas) are instantiated in (or identical to) parts of the world. Indeed Wittgenstein himself did make (fairly) similar points about these conflations of mathematics and the world. More specifically, Wittgenstein warned us against transferring what is applicable to (or true/false of) mathematical systems to the world itself.

As it is, Wittgenstein can be read as not actually questioning the logical validity or status of the mathematics. He was making a purely philosophical point about the (as it were) reading of mathematics into the world. Thus Wittgenstein’s position on mathematics and the world was largely down to his mathematical anthropocentrism. That is, to his belief that mathematics is a human invention. (More concretely, Wittgenstein once stated that “[w]e make mathematics”; and some time later he said that we “invent” mathematics.)

All the above means that if mathematics is a human invention, then any readings of maths into the world (or Nature) must be down to… us. And if they’re down to us, then these readings aren’t really telling us anything about the physical world — or even about a platonic world of numbers . And that’s simply because — according to both Wittgenstein and Smolin — such as thing doesn’t even exist.

[I can be found on Twitter here.]