Bertrand Russell on True Belief & Knowledge

 
According to Bertrand Russell (at least at one point in his career), not only is a belief not knowledge if it can't be substantiated with arguments, reasons or other beliefs, but it's not knowledge if it is derived from false beliefs which may have acted as reasons for the new belief.

So, in theory, I could derive the true belief that the earth isn't flat from the true belief that most swans are white. Clearly, in this case, there's no clear material connection between the two beliefs. If they weren't connected in some way by the subject, then such connections would have been either bogus or irrelevant – that is, not genuine connections.

This may be why logicians say that "from a true premise anything can be derived". That is, unless we require a material or relevant derivation from the true premise.

A true and materially connected belief for "The earth is not flat" may be "The horizon shows us that the earth is not flat’" Here, of course, there is a material and relevant connection with initial true belief.

Similarly, it's quite possible to deduce a true belief from a false belief. In this case, even if the false belief is somehow materially connected to the true belief, one still can't acceptably deduce a true belief from a false belief.

So, for example, we may derive from ‘Fish can fly’ the true belief that ‘Fish generally have scales’. Here there seems to be some kind of material connection in that both beliefs are about fish. But that isn't enough in this case.

For a start, they are about different aspects of fish. So, in that sense, there is still no genuine material connection. Also, we must repeat that one can't derive a true belief from a false belief.

In all these examples, it's clear that in order to gain knowledge, certain logical principles have to be adhered to. These principles guarantee knowledge.

For example, if the premises are true, then all correct inferences from these true premises must result in true conclusions. These true conclusions, then, would be examples of knowledge within a logical context. Of course the premises and conclusions must have material content and not just be examples of formal logic. That is, the premises must themselves be the conclusions of previous empirical investigation.

To have knowledge, according to the above, seems to mean that some kind of cognitive work has been done in order to reach a belief that is true. That is, Russell’s man is correct to believe that the then Prime Minister’s last name begins with B. However, this is because he thinks that the then Prime Minister was Balfour. In that sense, he was wrong. But he was, after all, only articulating a belief about the first letter of the Prime Minister’s last name. Though if he thought that Balfour is the Prime Minister, and the actual Prime Minister was Bannerman, then he clearly hadn't done any cognitive work to establish the first letter of the last name of the then Prime Minister. His true belief, therefore, was based on false knowledge. That is, he came to that belief for false reasons. Therefore he had no true knowledge.

To put this another way: Russell’s man had no justification for believing what he believed, even though what he believed is true. In a sense, his belief, though true, was based on pure guesswork. Knowledge, on the other hand, requires reasons for believing what one believes.

Though what if he did have reasons? He might have had the wrong reasons for believing his true belief. He might have thought, for example, that it was about time that a Prime Minister’s last name began with ‘B’. After all, up until then, no Prime Minister’s last name had begun with ‘B’. So, on his probabilistic reasoning, it was very likely that the Prime Minister’s last name would begin with ‘B’.

This kind of reasons is of course ridiculous. However, ridiculous or not, he might still have offered us reasons for believing what he believed. The problem is that they were simply bad reasons for believing what he believed. The problem now is: what would constitute, in this case, good reasons for believing what he believed about the then Prime Minister’s last name? This is, of course, another issue.

Does the above amount to saying that a belief can't be true, or can't be true knowledge, if it is believed for the wrong reasons? Similarly, a true belief may not be knowledge if it is produced by the wrong method:

"… a true belief cannot be called knowledge when it is deduced by a fallacious process of reasoning, even if the premises from which it is deduced are true. If I know that all Greeks are men and that Socrates was a man, and I infer that Socrates was a Greek, I cannot be said to know that Socrates was a Greek, because, although my premises and my conclusion are true, the conclusion does not follow from the premises." (131-2, Problems of Philosophy)

Are we to say that nothing is knowledge except what is validly deduced from true premises?

So it's not just false premises or prior beliefs that we need to watch out for; but also fallacious processes of reasoning. That is, there is more to reasoning that true premises and true conclusions. We could go from ‘Most birds fly’ to ‘Snow is white’; though clearly this would not instantiate a correct process of reasoning. However, is relying on the star charts or clairvoyance an example of correct reasoning simply because we take the premises to be true and the conclusion to be true? Russell's own example of faulty reasoning starts off with true premises and ends up with a true conclusion. However, no correct method of inference is used in this example: therefore the conclusion isn't an example of knowledge.

According to David Lewis, we can have examples of knowledge that don't depend on true beliefs, true premises or correct methods of inference. Sometimes we just know something and we don’t know why. For example, when we may have arrived at that piece of knowledge by justificatory reasoning in the past. Now, however, we have completely forgotten these cognitive processes; though we still, nevertheless, have knowledge.

Also, according to Lewis, we may have knowledge even though we haven't eliminated all possibilities of not-P, where P is our piece of knowledge. Lewis simply claims that it's impossible to eliminate all examples of not-P. Primarily because we are simply not aware of all examples of not-P. We couldn't be aware of all examples of not-P. In addition, some examples of not-P must be simply disregarded if we are to get the epistemic ball rolling.

For example, I believe that ‘snow is white’. But is it possible that my sensory receptors have inverted the colours I receive from the world due to a brain damage of some kind? Similarly, and more fashionably, I could be a ‘brain in a vat’ who is being fed sensory distortions care-of a mad scientist. Though I think that Lewis may see here that the brain in a vat hypothesis must be ignored ‘(proper ignoring’) simply because there is no known way of disproving that possibility. (Putnam does claim, however, that it is possible to prove that we aren't brains in a vat.)

There are similar sceptical stratagems that, according to certain epistemologists, we can't disprove. And in many cases, the reality of the sceptical challenge is essentially indistinguishable from the non-occurrence of the sceptical possibility.

Bertrand Russell himself gave the example of the earth being created five minutes ago with all its examples of fossils and remains exactly as they would be if the earth had been had it been around for billions of years. Though because the differences between the sceptical possibility and the present actuality are zero, it's simply counter-productive to take these sceptical challenges seriously. Again, if not-P were taken seriously, we couldn't get going in any epistemic process. Not only is there a possible infinite amount of not-Ps, but some not-Ps are deemed, by some, to be basically nonsensical.

Richard Rorty on Analytic Philosophy’s a Priori

What is it, precisely, that Richard Rorty thinks analytic philosophy is trying to achieve?

Let us take the ‘linguistic turn’ for starters. The aim of philosophers at that period (according to Rorty)

"was to mark off a space for a priori knowledge into which neither sociology nor history nor art nor natural science could intrude". (EHO)

Basically, Rorty believed that philosophers were trying to find "a space" for themselves. They wanted their own playground. That's why they needed a priori knowledge: that is, non-empirical knowledge. The things which only needed a philosopher’s brain and nothing more than a good armchair.

This was part of a long tradition.

Take Kant.

Before the linguistic turn, Kant had formulated his own "transcendental standpoint". In Kant’s case, it was the mind which provided us with the a priori limits of experience. Then it was meaning – or language – which provided all that is a priori. If language or meaning can offer us with the a priori, is that the same thing as claiming that the mind does too?

Donald Davidson also spoke out against this a priori notion of language or/and meaning. He wrote that we

"must give up the idea of a clearly defined shared structure which language users master and then apply to cases." (‘A Nice Derangement of Epitaphs’).

What can language as a "clearly defined shared structure" possibly mean? It sounds as if Davidson thought that philosophers are treating language - or a language - as some kind of quasi-object or entity. Thus such philosophers were reifying language it as if it is there – as a given – before people actually used it. That is, as something with necessary structures which are out of people’s control.

Surely, then, it must follow that the invariability of language’s givens must flow from the invariants of minds. Where else could language - or a language - come from? If we can ‘master’ language, then it must already be there. This is saying more than the fact that language is passed on from adults to children. In a sense, it's passed onto adults; who themselves pass it on. 

We can imagine the logical constants being, well, constant - as some kind of given. Perhaps certain inferential relations between propositions too. Though it's still hard to understand - without examples - what certain philosophers mean by the word ‘language’.

Logicism

Frege's prime purpose for writing his well-known and important Foundations of Arithmetic was to show us that mathematics is really analytic; as well as to disprove Kant’s view that it is synthetic a priori. In that, Frege was at one with Hume. This analyticity of mathematics, according to Frege, could only be proved and shown by reducing mathematics to the elementary laws of logic – hence ‘logicism’.


Frege took these logical laws to be more basic than any truths and laws in mathematics because they "must be accepted if there is to be reasoning at all" (385). It can be said, therefore, that Frege’s position on the logical laws is not unlike Aristotle’s on his ‘laws of thought’ which are required in all reasoning, even reasonings which deny their truth or dispute their fundamental nature.


Interestingly enough, Leibniz was basically a proto-logicist. He provides these proofs that arithmetical statements can be expressed logically:


2 = df. 1+1
4 = df. 1+1+1+1
Therefore:
2+2 = df. 1+1+1+1 = 4


As can be seen, however, Leibniz still uses numbers in his ‘logical’ reductions of numbers and arithmetical statements. In a sense, every reductionist logical definition only uses the number 1, along with the equality sign and other operators.


However, surely 4 + 2 = 6 is more illuminating than 1+1+1+1+1+1 = 6 because that too could become 1+1+1+1+1+1 = 1+1+1+1+1+1 and so on.


In one sense Leibniz is also committed to a proto-extensionalist logic in which numerals can be substituted within an arithmetical statement if the substitutions have the same extension – the same number – as its extension.


However, Leibniz’s reduction does not function as correct classical logic because it misses out the brackets needed in his:


2+2 = df. 1+1+1+1


It should be this:


2+2 = df. (1+1) + (1+1)


In other words, without brackets we don't recognise the logical scope of the original arithmetical operators in their statements. That is, 2 = df. (1+1), not 2 = df. 1+1. Similarly, 2 + 2 = df. (1+1) + (1+1), not the initial 2+2 = df. 1+1+1+1.


S puts it this way: "What entitles us to drop the brackets and convert (1+1) + (1+1) into (1+1+1+1)?" (386). The operation + enables us to add 2 + 2, so 1+1+1+1 isn't allowable because it is 2 that is added to 2, not 1 + 1 that is added to 1 + 1. Not only that: these brackets show us the scope of the arithmetical ‘2’ in terms of the operator of addition. So if Leibniz reduces it to 1 + 1+ 1 + 1 only by illicitly or tacitly using a mathematical operator in his ‘reduction’. And if he has done that, then he has not reduced arithmetic or mathematics to logic at all (just as a Tarskian meta-language cannot use terms from the object-language).


Other Reductions


Dedekind, at the end of the 19th century, reduced the basic notions of arithmetic (rational, real and complex numbers) to the theory of natural numbers, if not to logic itself. Of course we need to know what natural numbers are, and how they differ from rational, real and complex numbers.


Peano too reduced arithmetic to a set of axioms. Peano’s ‘postulates’, of course, are far better known than anything offered by Frege or Dedekind, for example. What are Peano’s postulates or axioms? These:


i) 0 is a number.
ii) Every number has at least one and at most one successor which is a number.
iii) 0 is not the successor of any number.
iv) No two numbers have the same successor.
v) Whatever is true of 0, and is also true of the successor of any number when it is true of that number, is true of all numbers.


It can be seen that Peano’s postulates are intuitively acceptable and also very simple in nature. Presumably he said that ‘0 is a number’ because other mathematicians and philosophers didn't actually think this.


In terms of postulate number ii). If every number has one successor, then this by definition seems to create or accept an infinite class of numbers. In addition, if the number 0 is not itself a successor of a number, then Peano must have rejected negative numbers like -1 and -44 and so on. They must have come later, as it were.


However, postulate v) seems to be incorrect. It says that whatever "is true of 0… must be true of all numbers". But postulate iii) has already claimed that "0 is not the successor of any number". Not being a successor, then, is a property of 0, so how can ‘all numbers’ have the same properties as 0? More correctly, how can the statement "whatever is true of 0… is true of all numbers" be true? If not true, then correct according to its other fellow axioms, specifically axiom three.


The last axiom just stated, interestingly enough, is the ‘ell-known axiom of mathematical induction. In other words, we have a strange juxtaposition of induction and a mathematical axiom. This is especially interesting because many philosophers and logicians say that the so-called ‘logical law of induction’ is not a genuine logical law at all, primarily because it deals with probabilities and not necessities and also, for example, because induction is a psychological phenomenon; at least according to Wittgenstein.


Anyway, the fifth axiom is inductive in nature because it "enables us to prove theorems about all the numbers by considering only three of them" (386). In other words, what is said to be the case in three of Peano’s axioms can be used inductively to show why the other two axioms are true, and also true about the nature of all numbers. So the axioms themselves, when taken separately, are themselves a micro-deductive or inductive system in that it has two ‘meta’-axioms, from which two lower axioms, as it were, can be deductively derived. And when we have all Peano’s postulates together, then we can again derive things; though this time theorems, not more axioms. Indeed not only can the axioms engender theorems and also two more axioms, but what is said or stated in them about numbers provides the basis of a mathematical system in which pure numerical axioms can be used to derive more numerical theorems from them (just as logical premises engender conclusions).


According to Peano’s postulates, all of arithmetic can be derived from them.


Are his postulates logical in nature?


In terms of logicism, the logicist seeks to define the three primitive terms – ‘number’, ‘successor’ and ‘0’ – and show that the postulates can be derived by logic from the definitions. So, in that sense, Peano carried on the programme begun by Frege a few decades earlier.


How were the primitive terms shown by Peano and the logicists to be explainable in terms of logic and logical terms?

Propositions, Facts & Sentences

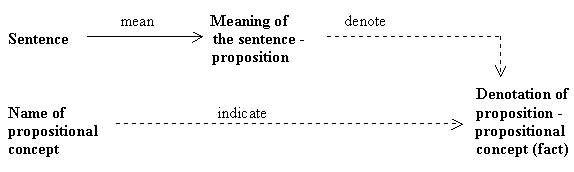
Different Sentences = Same Proposition

The popular and general idea (at least in Anglo-American analytic philosophy) is that if no particular expression of a proposition is identical to that proposition, then the proposition must be distinguishable not only from a specific expression of it, but from all expressions of it. The argument is usually that a proposition is distinguishable from a particular expression of it. However, perhaps the truth is that it's the sum of all possible linguistic expressions of it. That is, when all possible expressions of the proposition are in, then there's nothing left out of the proposition. There's nothing else to say about it. And if there's nothing else to say about the ostensibly expression-independent proposition that hasn't been said by the sum of all its linguistic expressions, then perhaps there's no distinction between them at all.

It's argued that propositions don’t belong to a particular language or even to the set of all languages. I would say that they do belong to the set of all languages (or to language itself). Clearly we can't believe in abstract propositions simply because the French words for "I love apples" or "The day after tomorrow" are different from the English words already given.

Proposition realists ‘explain’ the existence of the fact that "co-referential" sentences may have different truth-values by referring to pre-existent or eternal propositions. However, the only things you can say about these propositions (or the differences they may express which aren't explicit in the sentences themselves) is with yet more sentences (with, perhaps, different truth-values).

Despite the fact that many different sentential expressions can express the same proposition, it's still nevertheless the case that we never actually come across a proposition as it is free from - or independent of - sentential expressions.

We can say that a proposition can indeed be variously expressed by many expressions. It also follows that an expression can also be variously expressed by other expressions. In that sense, E (expression) can take the place of P (proposition). Now we can say that an expression can be variously expressed by various expressions as well as the expression that we initially took to be the proposition. In that sense, the proposition is only an expression that has somehow been given a special status. It can be said that a proposition is the sum of all the possible - and actual - expressions which assert the same thing. However, in principle we could account for all the various expressions of a given statement. Any that go unaccounted for will still be expressions of some kind. In addition, I stress the proposition/expression above precisely because it's an expression (this time) that's been given a special status.

The key question is:

Can the content of a proposition be separated from the form of that expression?

What sort of existence and identity does a proposition have before it finds itself ‘in’ an expression? Do we ever have the content of a statement before the statement itself? 

It can be admitted that what constitutes a proposition (facts, truth-conditions, abstract objects, possible worlds.... take your pick) exist separately from all sentences; though not the proposition itself. Books can exist separately from libraries; though when they're brought together, they constitute a library (but were not themselves libraries before they were brought together).

Many mind-independent things may be necessary for propositions; though only these things plus sentences (or expressions) are sufficient for propositions. This is what makes the proposition-realist make a mistake. Many of the constituents of propositions may indeed be mind-independent (or even abstract) and therefore separate - and separable - from sentences. Many proposition-realists therefore conclude that truth, truth-conditions, propositions etc. are separable from sentences.

The other way to defend to existence of propositions is that the same sentence can state different propositions. Or the same sentence "can have the effect of claiming, stating, or asserting different things". That, in itself, can't be an argument for the existence of propositions. A spoon can be used to eat soap of burn crack. Does that mean that we have two different things rather than one thing used in two different ways?

Michael Dummett goes into detail as to why Frege believed that there's such a distinction between a proposition and its linguistic expression – or, in Frege’s case, between a sentence and the "Thought" which it expresses:

"[A thought is] not true for you and false for me, it’s not true at one time and false at another time." 

The idea being expressed here is that it may appear to be the case that a Thought is true for me, though false for you; or true now, though false tomorrow. Yet that's only because its linguistic expression leaves something out. If expressions were more precise and more explicit, such things wouldn't be left out.

This leads us to the conclusion that the Thought itself is precise and explicit.

It's strange that something that is ostensibly completely non-linguistic can be both precise and explicit at all. How can something abstract and non-linguistic be precise and explicit? What does it mean for an abstract Thought or proposition to be precise and explicit? Surely only linguistic expressions can carry the requisite information that will allow a thought to be precise and explicit. How can it be precise and explicit with its – or any – linguistic expression? What would constitute its precision and explicitness?

So despite Dummett’s defence of the existence of abstract propositions, he acknowledges the fact that the proposition/expression dichotomy may not amount to much.

The amounts to the evident point that even if abstract propositions exist, what we say about them (or when we express them) evidently needs to be done with sentences. Thus we must "attach" truth to sentences even if it's really propositions which are the actual "bearers of truth". If it's the case that a sentence expresses a proposition, then it'll still be the case that that proposition will require (or need) a linguistic expression. Thus truth, again, must also be attached to sentences; not just to propositions. (If we can really attach truth to abstract entities at all.) However, Dummett still insists in talking about the "interpretations" of propositions. As I said, the fact of multiple and variable interpretations doesn't lead him away from propositions, but towards them.

Facts aren't Bits of the World

Many people take facts to be bits of the world to which true propositions somehow correspond. Many would disagree with the suggestion that facts are not bits of the world or that they are linguistic or sentential in nature. After all, isn’t it the case the proposition "Gordon Brown is PM" is true because of the bit of the world that is Gordon Brown’s being Prime Minister (among other things)? But facts are not just particulars or bits of world. They're arrangements (as it were) of bits of the world and also what's said about these arrangements. Michael Loux puts this in the following more metaphysical less semantic kind of way. He says that

"we cannot completely and adequately identify that in the world which makes a true proposition true merely by listing the various particulars and attributes (properties, kinds, and relations) that populate the world". 

In that weren't the case, there would literally be an infinity of possible facts. For example, the fact that Paul Murphy is two foot away from that blackboard; the fact that two black shoes are next to two white shoes; Or even that one million planets do not have water on Tuesdays. Indeed it's even a fact that  there are nth amount of specs of dirt on my computer screen; though yesterday there were ten less.

Even this infinity of possible facts inn't the only argument because we can say that despite this possible infinity, they're still nevertheless facts. The factual aspect, however, is more to do with what's said about these bits of the world (whether planets, specs of dirt or blue shoes). In terms of the specs of dirt on my computer screen, we can say that these specs of dirt were indeed bits of the world before anything was said about them; though there were no facts about them until such facts were stated.

Someone may now say that particulars like Gordon Brown aren’t factual on their own. However, we've already referred to the property of his being Prime Minister. Some may say that included in facts are universals, properties and their connections. Particulars, universals and connections on their own don't make facts either. It all boils down to what we say about these particulars, their properties and relations. Or, more specifically, it boils down to the linguistic situation that before we offer up our fact we must state something like: "It is a fact that…" Or: "It is the case that..." This shows us that facts are to do with sentential or mental attitudes towards particulars and their attributes and relations, not just the latter on their own. Particulars, attributes and relations are just bits of the word on their own. They aren't facts, not even when they belong together as bits of the world.

Facts as True Propositions & True Propositions as Facts

The proposition (or how the proposition is stated) is exactly the same as the fact which is supposed to make it true. Thus we have a kind of tautology (or an actual tautology). Of course the proposition

"Gordon Brown is PM."

is true because of the fact that Gordon Brown is PM.

Or more precisely:

The proposition "Gordon Brown is PM" is true because of it is a fact that Gordon Brown is PM.

Many philosophers actually say that "a fact is a true proposition" (e.g. Dummett). Thus we have this example of circularity:

fact = a true proposition

and

true proposition = a fact

Thus a true proposition just is a fact or a fact just is a true proposition. But facts "are supposed to be entities correspondence to which makes true propositions true" (168). They're supposed to be bits of the world. Thus if facts are true propositions, then either true propositions are bits of the world or facts are - as propositions - not parts of the world. Indeed it's easier, on this view, to accept that facts aren't bits of the world than it is to accept that propositions are bits of the world – which no one accepts. If we correlate facts with true propositions, and true propositions with true sentences, then we can indeed accept that facts aren't (only) bits of the world. (However, in a sense, sentences can be taken to be bits of the world.)

It follows that many will want

"a purchase on the notion of a fact that is independent of our understanding of the concept of a true proposition". 

Put it this way:

Q) What is it to say that this or that is a fact?

A) Is it not just to say it is true?

That is, if facts can be true, then doesn’t that mean that they must be sentential or at least propositional? After all, how can the bit of the world that is Brown’s being PM be true? What is said about Brown can be true; though not only his being PM. That would be like saying that the cup in front of me "is true".

Again:

i) Thus, to say that it is a fact that (or: it is the case that) Brown is PM. 

ii) is to say neither more nor less than that it is true that he is.

Facts are supposed to be what make propositions true. They surely can't be true themselves. If not, the fact that is true is making a proposition or sentence true. This doubling-up effect can be countered by accepting from the beginning that facts are indeed propositional. Or, on this account, that facts are sentential. In that case, if true propositions and true facts are identical, let’s get rid of one of them. Let’s get rid of (true) facts. Now we have true propositions. I take these to be linguistic.

Thus let’s get rid of true propositions. This will leave us with true (or false) sentences or sentential statements. The problem with the linguistic nature of supposedly worldly facts can also be applied to the linguistic nature of abstract propositions. Facts were seen to be linguistic, thus we got rid of them. Abstract propositions also turned out to be linguistic and not abstract at all, thus we got rid of them too. Again, we are now left with true (and false) sentences or statements.

Loux, on the other hand, accepts abstract propositions; though he also accepts that we have a conflation or mix-up between true propositions and facts. He writes:

"... we can hardly claim to have provided an explanation of the truth of that proposition by introducing the fact that he is President. The two are one and the same thing!" 

We can’t say that the statement

"Brown is PM of the UK."

is true by saying

"It is a fact that Brown is PM of the UK."

because the true proposition and the true fact are "one and the same thing!" (168). We think that Brown’s being PM of the UK is a bit of the world; though all it's actually doing is mirroring a true proposition which we have firstly constructed. I would say that the sentence, "Brown is PM of the UK" comes first.

Facts, Propositions and their Linguistic Expressions

We can go so far as to say that we "can only identify a fact through a proposition". This would mean that there are no facts without the propositions which express them.

What if propositions themselves can only be expressed through sentences?

Thus if it's correct to say that facts need propositions to be expressed, then we can also say that propositions require sentences in order to be expressed. Perhaps we can even forgo non-linguistic propositions and settle only with sentences or statements.

Can we also forgo facts?

We can if we've already forgone abstract propositions because, as I’ve said, facts require propositions and propositions require sentences. Thus, without propositions, facts simply require sentences to express them. It is sentences that individuate and determine what are the facts. Facts are as artificial as propositions. Thus all we have left are sentences which individuate and determine the parts of the world we wish to talk about. Without sentences, then, there would be no facts; just as there wouldn't be propositions without their sentential expressions.

Another reason for rejecting propositions is this. We

"can only identify a fact through a proposition: the proposition that my car won’t start, which can be 'nominalised' into the phrase 'my car’s not starting”’.

The problem is that is saying that "my car won’t start" is the same as "my car’s not starting". It is virtually the same sentence. We can see, then, that it's the sentence itself which individuates and determines the fact.

What we have, then, is the far from impressive conclusion that the "proposition that p is true if and only if it corresponds to the fact that p' (100). Surely, then, p is identical to, well, p – especially since they have the same content and are expressed in the same (linguistic) way. This may not be vacuous or contradictory. Perhaps we express what truth is in a way that "has to be that way". (As with Tarski’s T sentences.)

The end result seems to be that 

"it still remains true that to identify the thing that makes a proposition true, we must offer a proposition". 

It's a proposition that makes a thing true. Even if that proposition is abstract, it still requires a linguistic expression. And the linguistic expression we use for the proposition is the same linguistic expression we use to express the fact (or truth-condition) which makes it true!

Despite all that, Roger Scruton, for example, argues (in a realist spirit) that the

"proposition that p might never have been formulated; but still the fact that p would exist".

If proposition p might never have been formulated, that must mean that Scruton believes that it's mind-independent. If it's mind-independent, then it's also abstract and non-spatiotemporal. But the fact that it expresses must also share this property of being abstract and non-spatiotemporal because Scruton says that if the proposition hadn't been formulated, "the fact that p would exist’". Aren’t facts bits of the world? Yes. But I've already said that they're linguistically individuated and determined. Scruton says that they can exist without their propositional expression. If propositional expressions are by nature linguistic in nature, and therefore so too are facts, then how can there be any facts which haven't been given a linguistic expression? There can be no relation between a proposition and a fact that makes it true if that proposition is linguistically expressed in a way that relates to the fact and makes it true.

Scruton then writes that in

"comparing our propositions with the facts, therefore, we are comparing them with something other than themselves". 

Of course there's something other than propositions or statements about this something. However, it is sentences that determine and individuate the shape (as it were) of this something in the world. Only then can we call them ‘facts’. I'm not saying that bits of the world are sentences. Only that sentences determine and individuate what it is we take to be a fact; otherwise we only have a nondescript part of the world which hasn't been individuated or even determined. Thus this non-individuated and non-determined part of the world can't be a fact. It can only be a fact through its determination and individuation by a proposition – therefore by a linguistic expression.

Scruton doesn't accept that propositions are linguistic expressions. Though he does seem to accept that propositions and facts may be identical. He says that

"we seem to have no other way of identifying facts, save through the propositions that they are supposed to anchor". 

I would suggest that the suspicion Scruton shows about any real distinction between facts and propositions can be carried over to a suspicion about any real distinction between propositions and their linguistic expressions. Thus it follows that if we can't have facts without propositions, then neither can we have facts without linguistic expressions.

Scruton asks this about propositions and facts:

"Why are we sure that we have two things, when both are identified in the same way?" 

Now I will ask:

Why are we sure that we have both propositions and their linguistic expressions when both are identified in the same way?

If we can't break off facts from propositions, perhaps we can't break off propositions from their linguistic expressions. Or, more radically, perhaps there are no propositions.

Does this mean that there are no facts?

No, there are facts; though they aren't mind-independent and they're always individuated and determined by linguistic expressions.

In fact we can't even say "by their linguistic expressions" because this would seem to suppose that they somehow exist before their linguistic expression (or their linguistic individuation and determination). Facts, like the numbers of the intuitionists, "spring into existence" when they're linguistically expressed or individuated and determined by linguistic expressions.

Conclusion

Why isn’t the proposition-realist at least a little suspicious of this tight fit between propositions and the sentences which express them?

The realist could say that he must express propositions in some way. And the only way available to him is through sentences. I can still ask:

Yes; though do these sentential expressions of propositions precisely capture or match the propositions which they're expressing?

If his answer is, yes, then I can again ask:

Isn’t this strange – this perfect fit (or match) between propositions and the sentences which express them?

Why is it the case that sentences (or all the sentences which express proposition) can (as it were) miss something out of the proposition they (try to) express? However, this possible ambiguity, vagueness or imprecision of our sentential expressions isn't often acknowledged by proposition-realists. More than that: considering the importance they give to propositions (in terms of truth, certainty and objectivity) these possibilities would be anathema to them and would defeat the object of abstract propositions. That object, historically, has been that propositions are the guarantors of truth, objectivity and certainty.

At the heart of Derrida’s early philosophy of language is the thesis that there's no proposition beyond or behind the sentence – beyond language. Language is the beginning and the end of propositions:

"It [writing] is also to be incapable of making meaning absolutely precede writing…" (‘Force and Signification’, page 10, Writing and Difference, 1967/1978)

According to Derrida, "writing" doesn't simply transcribe something that already exists – a proposition. Propositions can only exist as expressions – in the guise of language:

"To write is to know that what has not yet been produced within literality has no other dwelling place, does not await us as prescription… Meaning must await being said or written in order to inhabit itself..." (1967/78)

Derrida then quotes Merleu-Ponty:

"Communication in literature is not the simple appeal on the part of the writer to meanings which would be part of an a priori of the mind… 'My own words take me by surprise and teach me what I think,' he said elsewhere." 

Propositions have been deemed to be necessary entities that help us secure certainty and absolute correctness. If we tune ourselves into the proposition, then we'll get things right. They help secure us from empirical vicissitudes and uncertainty. They are the "centers" (Derrida, 1967/78) around which all contingent and empirical expressions gravitate (see Dummett).

This is the old Platonic worry.

There must be propositions otherwise we'll succumb to relativism, uncertainty and other such things.

Perhaps it would be nice to have various centers or "sites" of various descriptions. Only then could dispute be stopped.

Abstract propositions, like universals and forms, would supply us with a means to find the correct meanings of our sentences. They would give us something determinate and precise for our contingent statements or sentences to be about. Thus we could find the true and correct answers to numerous philosophical and non-philosophical problems.

Abstract propositions guaranteed truth, correctness and certainty.

Vagueness & Ambiguity in Continental Philosophy

 
Julian Baggini offers some defences of what he calls "vagueness and ambiguity". He says that they could be "actually great virtues in writing because they open up possibilities" (59).


Can’t you ‘open up possibilities’ without ‘vagueness and ambiguity’?


Take the first quantum physicists.


Were they vague and ambiguous in their writings? Was Einstein? Was Gödel? In philosophy, were the radical ideas of Quine expressed vaguely or ambiguously? Of course not. I’m not even sure how vagueness and ambiguity actually ‘open up possibilities’ anyway. What does Baggini mean by this? The other point is this. Are we talking about intentional or unintentional vagueness and ambiguity? I suspect that Alan Sokal’s arguments are against the intentional ambiguities and vaguenesses of writers like Irigaray, Lacan and Delueze. That’s the point! It probably is intentionally vague and ambiguous. Of course vagueness and ambiguity may be a result of the complexity and difficulties of the subject-matter, say, in quantum mechanics again. This may not be the case with the writings Sokal is arguing against. That is, these writers go out of their way to make their writings seem complex and difficult precisely through their vague and ambiguous prose-styles. What about poetry then? –


"Well in poetry it’s a great virtue, in novels it might be a great virtue. But I do think that in analytical writing, whether it’s about physics or biology or history or sociology, the goal should be to remove ambiguity when possible. Of course, natural language is unavoidably ambiguous, but we should do our best." (59)


Perhaps Irigaray, Lacan and Delueze think that their writings are poetry. Or perhaps they think they are poetry and science or poetry and philosophy or poetry and philosophy and science. I don’t think that they do think that their writings are poetry or examples of literature; though Jacques Derrida, for one, might have thought this.


The question is: Is the ‘ambiguity’ an ‘unavoidable’ result of what it is they are writing about or it is the result of the author’s pretentiousness and gimmickry?


As Sokal concedes, "natural language is unavoidably ambiguous" (59) and so too is writing about complex and difficult issues in science, philosophy or wherever. However, do Irigaray, Lacan and Delueze "remove ambiguity when possible" or do they not even attempt to do this? More to the point, do they go out of their way to fabricate ambiguity and vagueness in order to make their writings seem complex, difficult and deep?