The cognitive psychologist Donald Hoffman doesn’t beat around the bush when it comes to how deeply mathematical he believes his own philosophical idealism to be. More relevantly, and perhaps more fairly, Hoffman believes that his notion of a conscious agent is deeply mathematical.
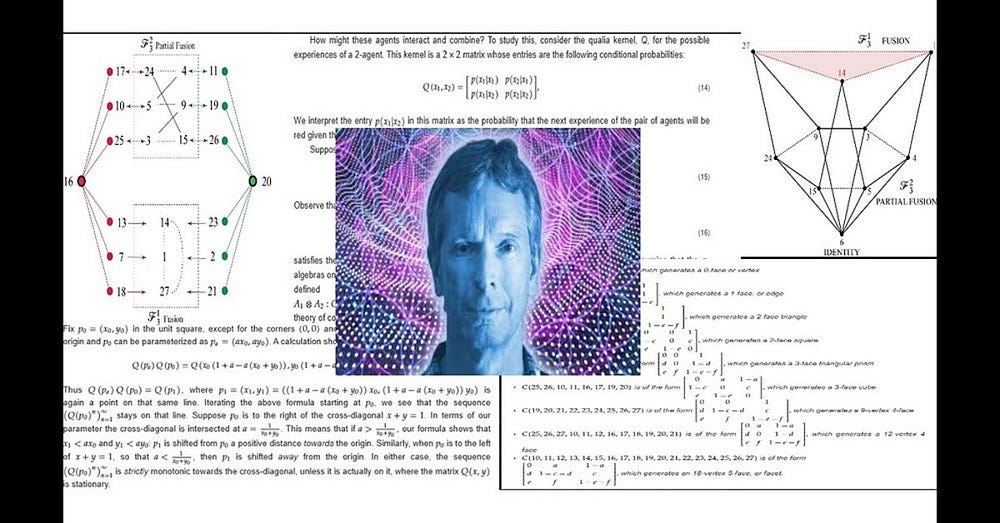
In his paper Objects of consciousness, Donald Hoffman writes:
“Thus the formalism of conscious agents provides a complete framework for computationally rigorous models of perception and cognition, and a rigorous solution to the so-called combination problem of consciousness, i.e., the problem of combining conscious experiences and conscious subjects [].”
Hoffman also states that his work provides “a precise hypothesis that, of course, might be precisely wrong”. He continues:
“We can explore its theoretical implications in the normal scientific manner to see if they comport well with existing data and theories, and make predictions that are novel, interesting and testable.”
So in what way is Hoffman offering a “precise hypothesis”?
And a precise hypothesis of what?
Hoffman’s Technicalese
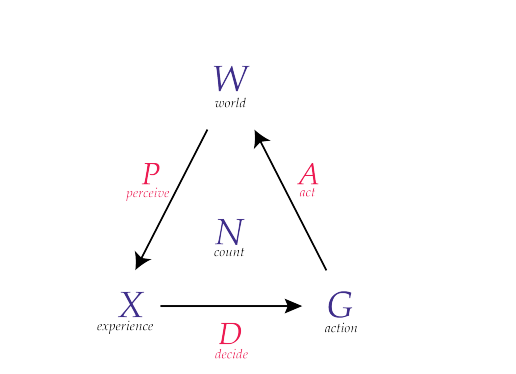
In his paper ‘The Origin of Time in Conscious Agents’, Hoffman writes:
“Informally, a conscious agent has six components, as illustrated in Figure 1. A conscious agent has a space X of possible conscious experiences and a space G of possible actions it can take.”
Although Hoffman does use the word “informally” at the beginning of this passage, readers should still ask questions about his choices of numbers, scientific terms, symbols, etc.
Now, informally or not, why six components? Why not seven, one, or two million? (It’s of course possible that Hoffman will concede that his choice of six is arbitrary.)
And what, exactly, is “space X”?
Are readers told what exactly space X is when Hoffman goes on to write that it’s a space “of possible conscious experiences”?
Again, what kind of space is this?
[Bear in mind here that Hoffman believes that “spacetime is doomed”, and he uses this idea to advance his idealism.]
And what are possible conscious experiences?
Indeed, even if space X is an abstract space, is this abstraction related to anything physical? (Since Hoffman is an idealist, this may be a silly question.)
Similarly, what is “space G” (i.e., not “space X”)?
Again, does it help that Hoffman goes on to say that space G is “of [the] possible actions [a conscious agent] can take”?
What are possible actions? And how does Hoffman know anything about what possible actions a conscious agent “can take”?
Of course, if the entity Hoffman calls a conscious agent is entirely his own invention, then it must also be entirely down to Hoffman to tell us which actions it can take, how many “components” it has, etc.
So is all this entirely Hoffman’s invention?
In other words, are these “mathematical models” of things which Hoffman himself has invented?
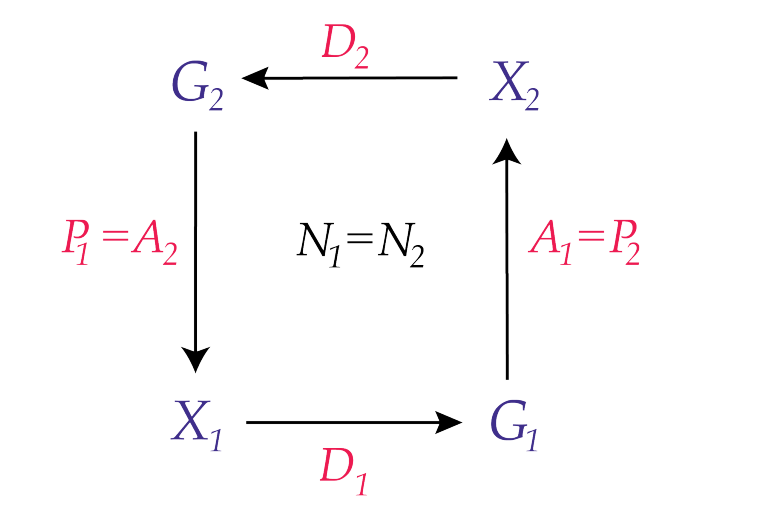
Tom McFarlane put Hoffman’s position in this way:
“Hoffman provides a precise mathematical definition of a conscious agent in terms of a set of experiential states X, a set of actions G, and maps that relate these to each other and to states of an objective world W (which itself is composed of conscious agents). The maps can be understood as defining the structure of perception P, decision D, and action A. Based on this definition, he constructs models of interacting conscious agents and derives predictions from those models.”
All that doesn’t help either.
[I’ve used McFarlane’s account because it’s much easier to understand than Hoffman’s own words.]
Apart from the fact that some readers may be deeply suspicious of all these references to a “mathematical definition”, as well as the use of the symbols X, G, W, P, D and A, we still aren’t told what a conscious agent is.
So does this “set of experiential states X” run free of a conscious agent? Do they (as it were) belong to a conscious agent? Are these events or actions of a conscious agent?
Again, all this doesn’t tell us what (as it were) underpins this set of experiential states X…
Perhaps nothing underpins experiential states X.
Exactly the same can be said about the words “a set of actions G”.
Surely set of actions G can’t run free of this conscious agent. Aren’t “actions” what this conscious agent does? So what is it, exactly, that’s carrying out these actions? And what is the relation between the conscious agent and this set of actions G?
More broadly, what is the rationale for this seemingly arbitrary set of experiential states X and set of actions G? Why are these two “sets” focussed upon, and everything else excluded? (Why do both sets contain the members they do contain, and not other members?) Indeed, why does Hoffman use these terms from mathematics at all?
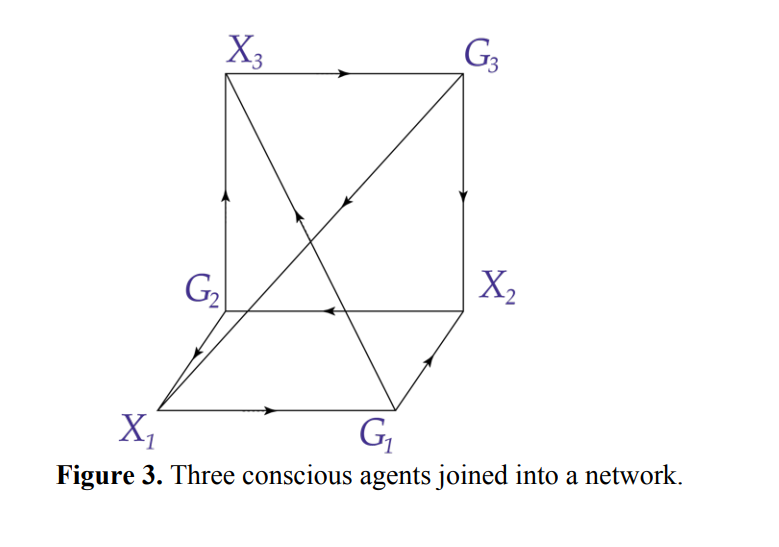
Finally, in the following passage (which is very hard to grasp), Hoffman provides us with yet more letters, numbers, symbols, mathematical terms and graphs:
“It perceives the world W via a perceptual map P, decides how to act via a decision map D, and acts via an action map A. The maps P, D, and A can be thought of as discrete communication channels. An integer N keeps track of the number of discrete messages transmitted over P. Figure 1. [] Definition 1. A conscious agent, C, is a six-tuple C = ((X, X), (G, G), P, D, A, N)), (1) where: (1) (X, X) and (G, G) are measurable spaces; (2) P : W × X → [0,1], D : X × G → [0,1], A : G × W → [0,1] are Markovian kernels; and (3) N is an integer…”
… And so on and so on.
Almost everything said abut the passages already commented on can now be said about this passage.
So let’s leave it there.
Conclusion

All the entities and terms in Hoffman’s philosophy are largely his own invention (even if to some extent based on existing scientific entities and terms). None of it has been made available to any scientists outside his own inner circle. Yet Hoffman is characterising a philosophical theory — a personal and speculative philosophical theory — as a scientific theory.
Compare this with another speculative philosophical theory: panpsychism.
On the whole, panpsychists don’t do what Hoffman does.
Panpsychists don’t claim that panpsychism itself a scientific theory — or even that it is scientific. It’s true that some (even most) panpsychists claim that their own brand of panpsychism doesn’t “contradict anything in physics” or that it’s “compatible with physics”. (As are all — or most — metaphysical theories.) However, they don’t claim that panpsychism itself is science or scientific.
Hoffman, on the other hand, at best says that his idealist speculations are scientific in nature. At worse, he claims (if sometimes implicitly) that it’s actual science. (He even refers to predictions, etc.)
So how does Hoffman attempt to make his (idealist) philosophy scientific?
That should be clear by now.
Hoffman attempts to make his (idealist) philosophy scientific primarily by using graphs, symbols, numbers, and terms from mathematics and physics, and then using and fusing all of them to advance his idealist philosophy.









No comments:
Post a Comment